离散小记2
离散数学
函数
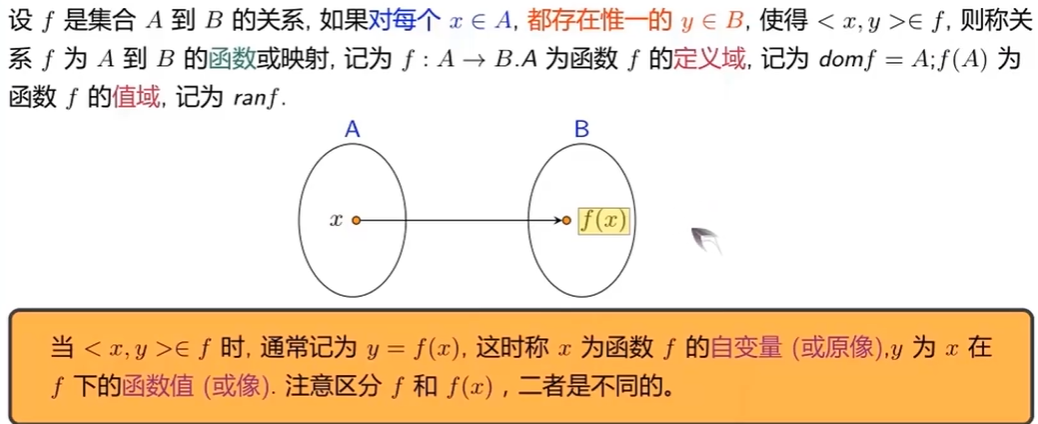
定义
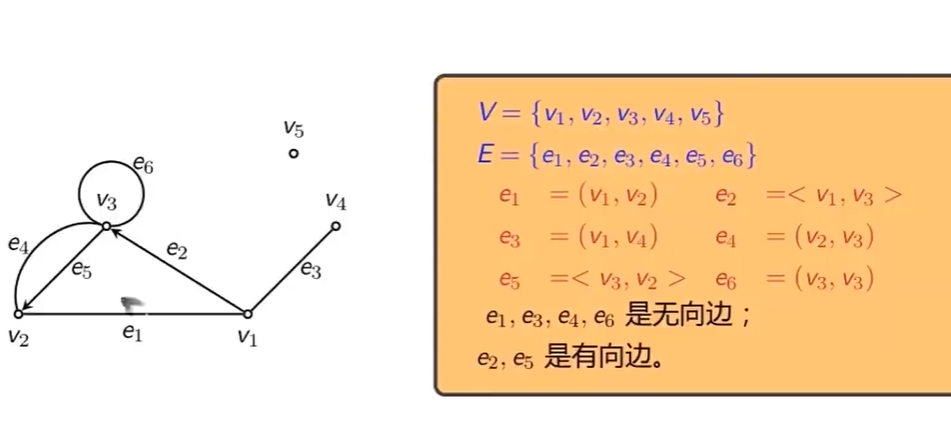
举例和函数集合表示
函数的数量
函数与关系的差别
数量不同:关系 - $2^{ A \times B }$,函数 - $ B ^ A $ 基数不同:每个关系和每个函数拥有的序偶个数不同,关系 - $0\to 2^{ A \times B }$,函数 - $ A $个。 - 第一元素:序偶中第一个位置的元素。关系中允许存在相同第一元素,函数则互不相同。
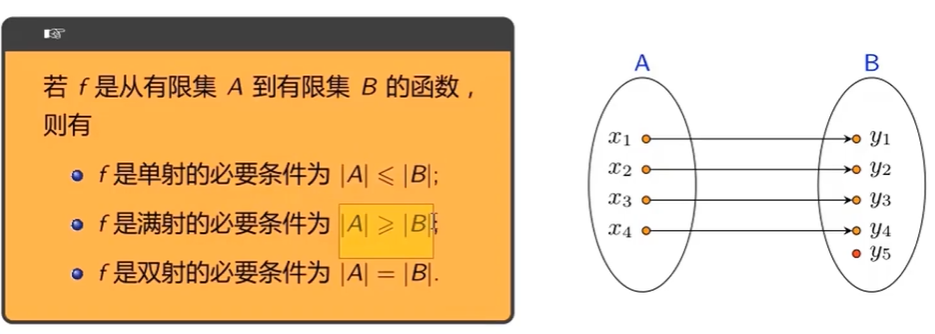
函数的类型
函数类型的数学化描述
数学化描述证明函数类型
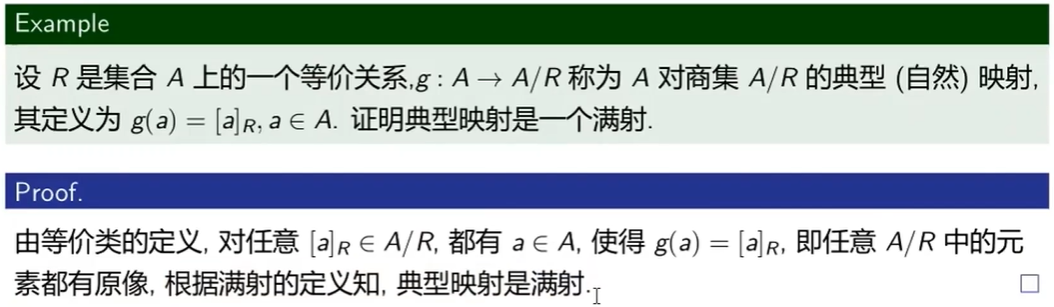
证明等价类到等价关系 - 满射
证明偏序集到幂集 - 单射、保序性
函数的运算
函数的复合
- f的后域(值域 Range) $\in$ g的前域(定义域 Domain)
- 恒等关系也是恒等函数,复合后可以等于自身
- 右复合法*
例子与性质
- 不满足交换律
- 满足结合律
复合运算的保守性
逆函数
图
图论从小游戏般的问题发展壮硕
- 哥尼斯堡七桥问题
- 周游世界问题
- 着色问题
- 迷宫问题
- 博弈问题
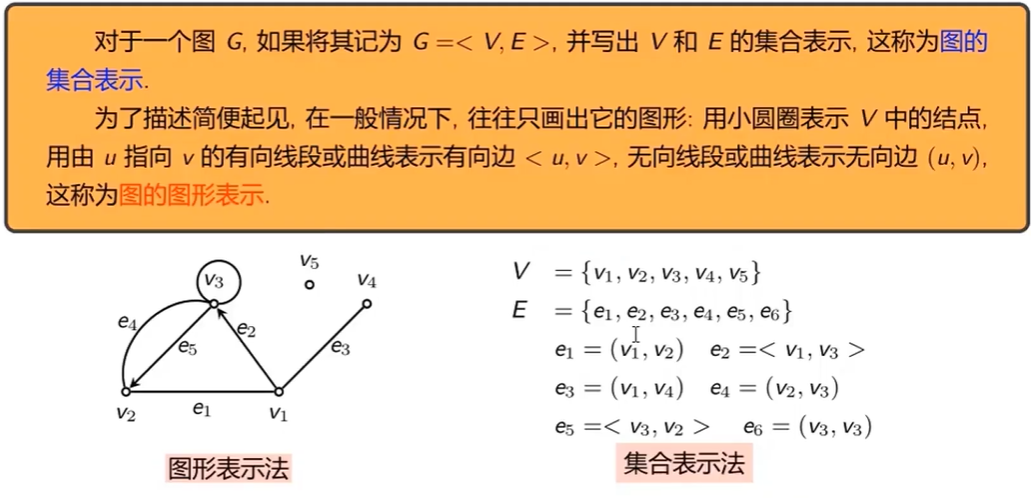
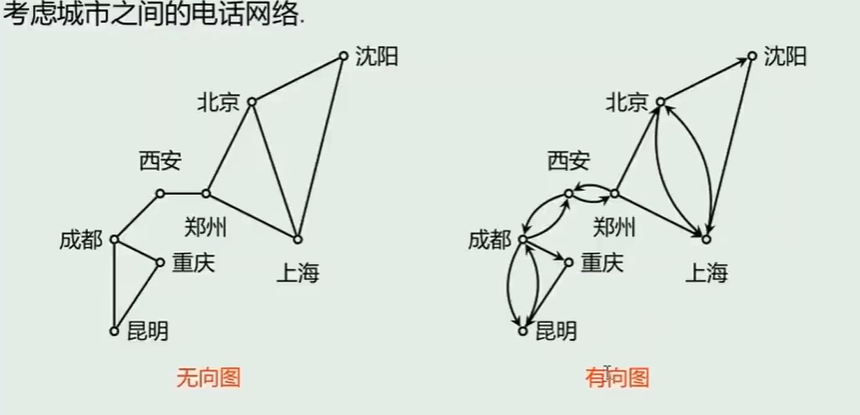
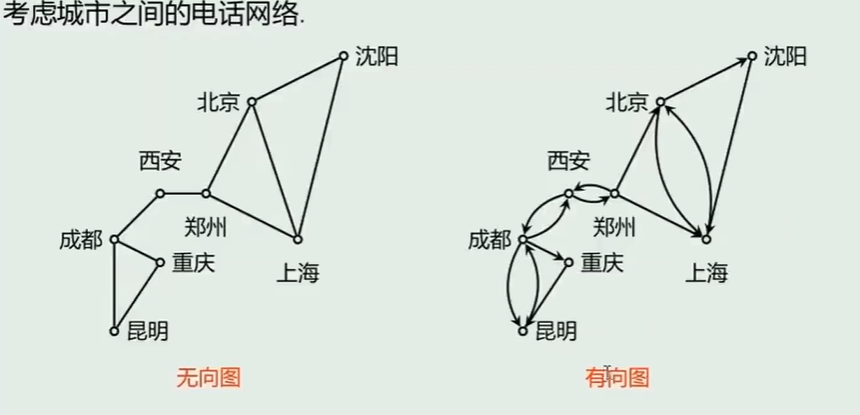
- 棋盘上马的行走路线 图的定义描述:图论中的图是指 某类具体离散事物集合和该集合中的每对事物间以某种方式相联系的数学模型。一个图就是有一个表示具体事物的点的集合和表示事物之间联系的一些线的集合所构成
表示法
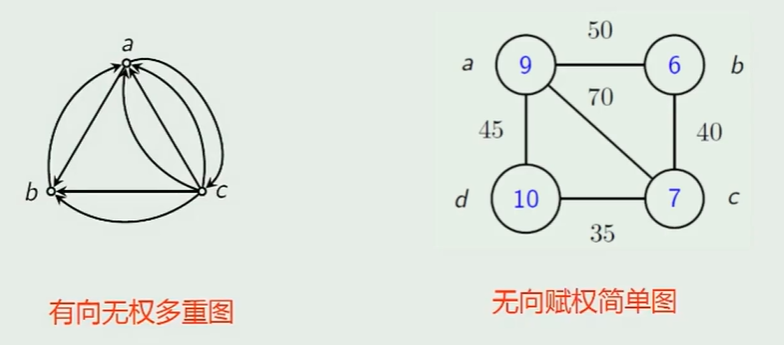
图形表示法
- 有向图
- 无向图
- 多重图
- 有环图
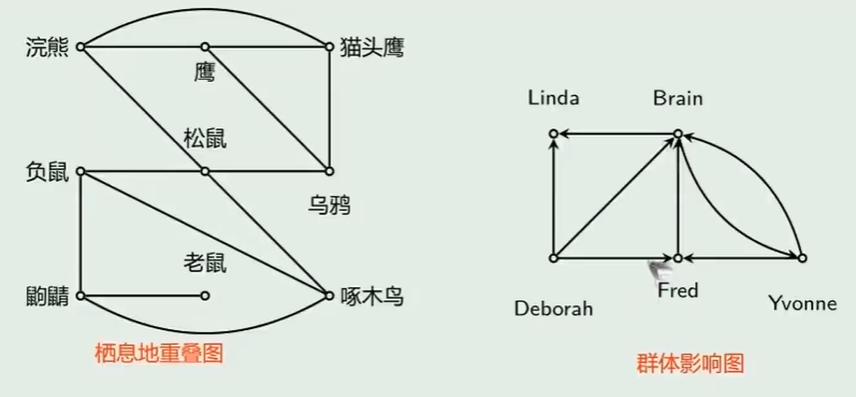
- 其它应用
- 栖息地重叠图
- 群体影像图
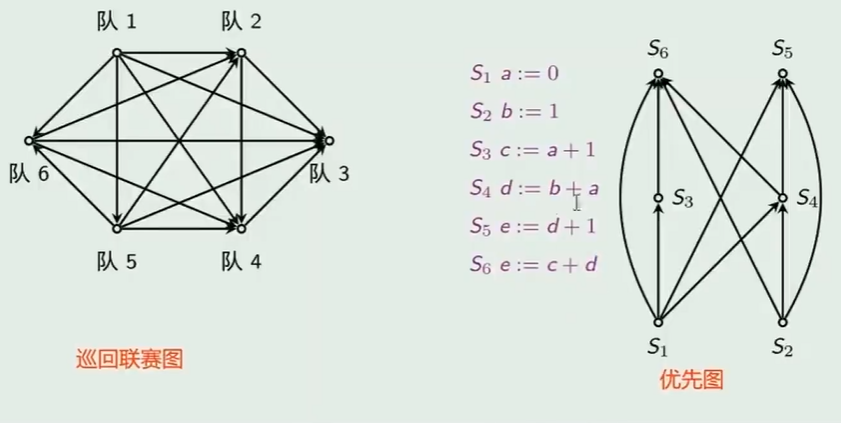
- 巡回联赛图
- 优先图(并行执行的关系图)
集合表示法
无序对和无序积
图的定义
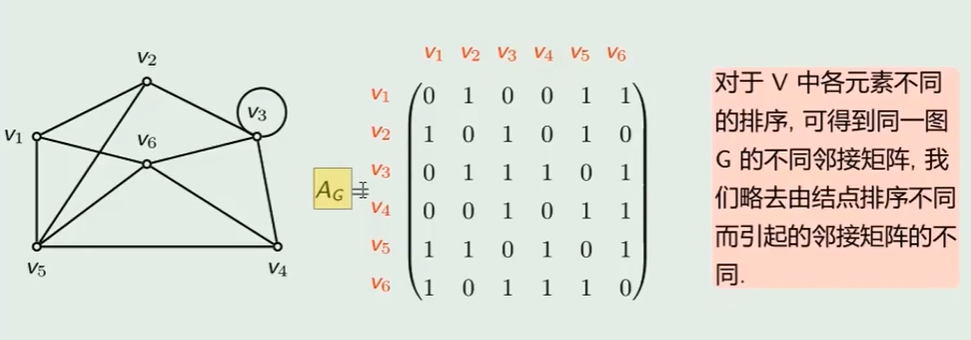
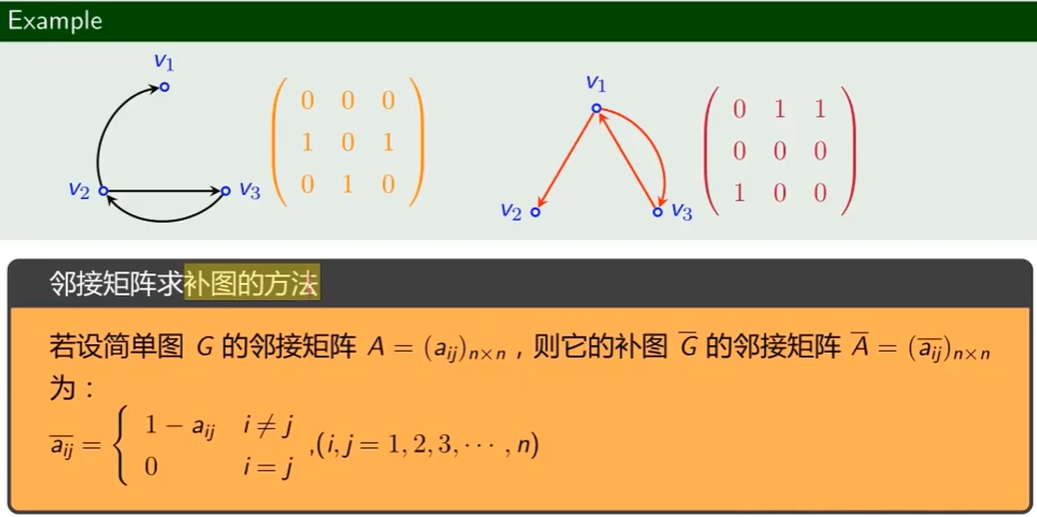
矩阵表示法
- 邻接矩阵
- 邻接点
- 邻接边 - 边之间的关系
- 环/自回路
- 孤立结点
定义
示例
邻接的定义
特殊图
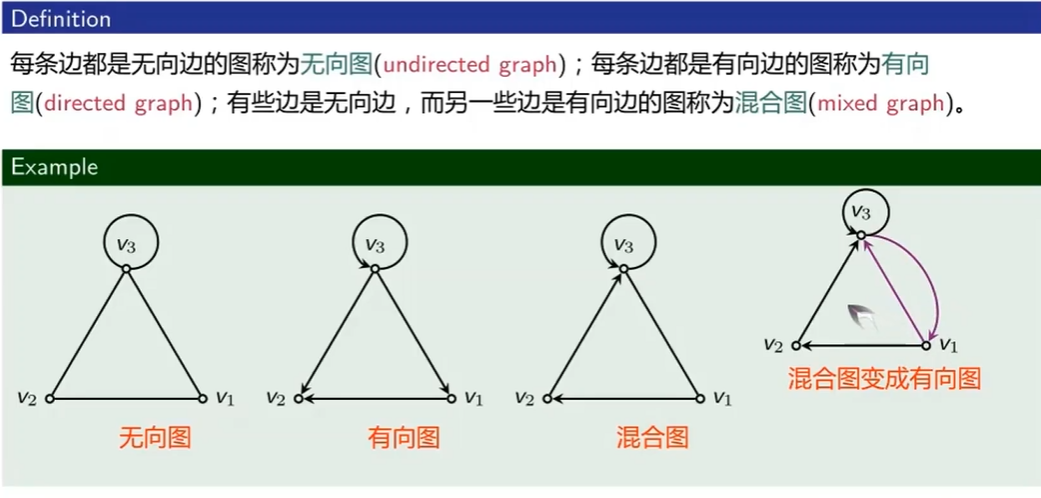
图的分类
按边
- 有向图
- 无向图
- 混合图
- 变成有向图的方法:将无向边变为方向相反的两条边
平行边
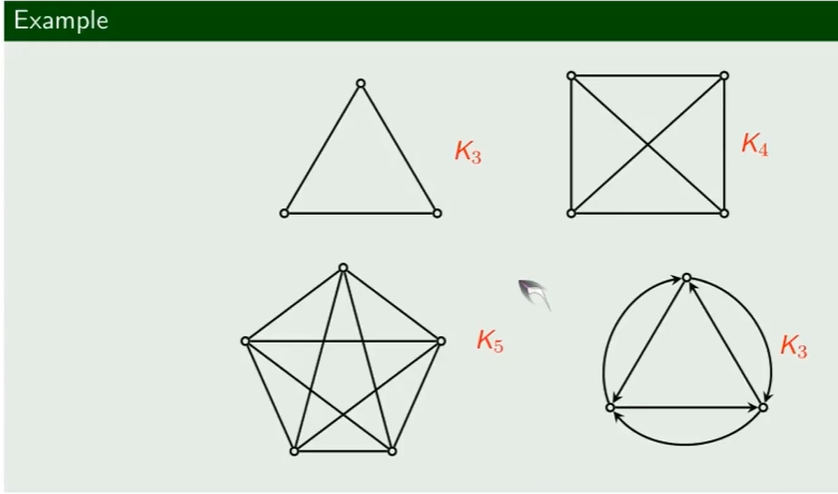
完全图
- 任意两个结点都有边相连的 简单图
- 有向图中:对边的要求是两条方向相反的有向边
- 对于 n个结点 的完全图,有几条边
- 无向完全图: n个结点中,可任取两个连成边,即 $C_n^2$
- 有向完全图:任取两个结点,可连成两条边,即 $2\times C_n^2$
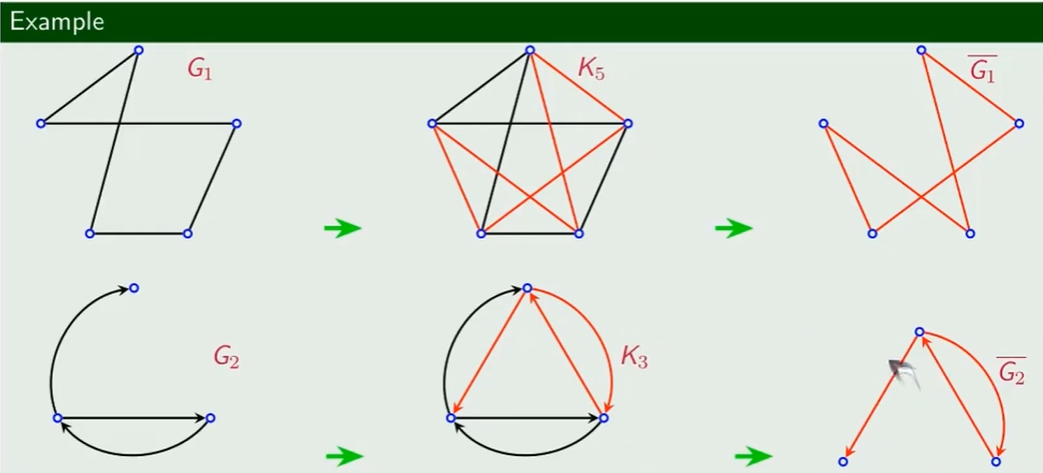
- 由完全图引出 补图
按权值
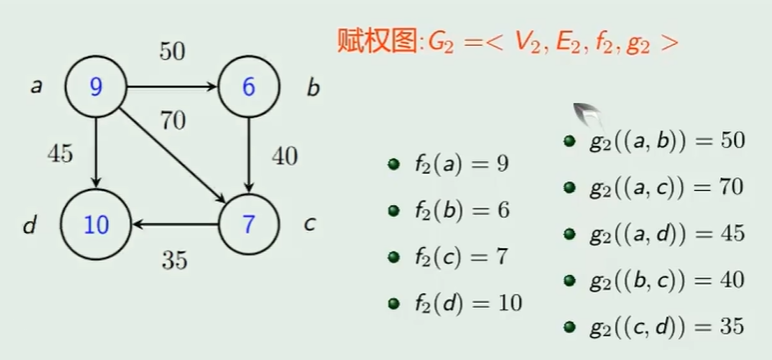
赋权图
例子
实际应用
分类方法
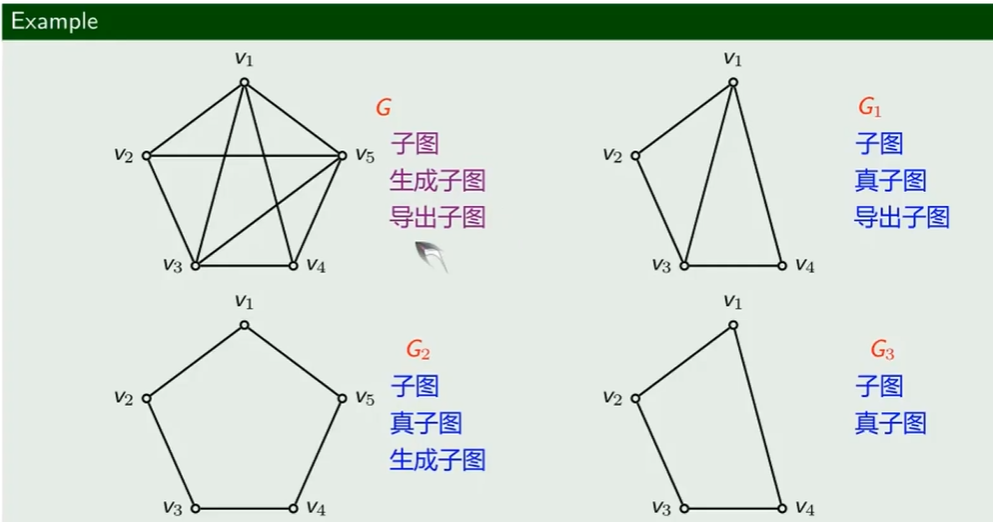
子图
子图示例
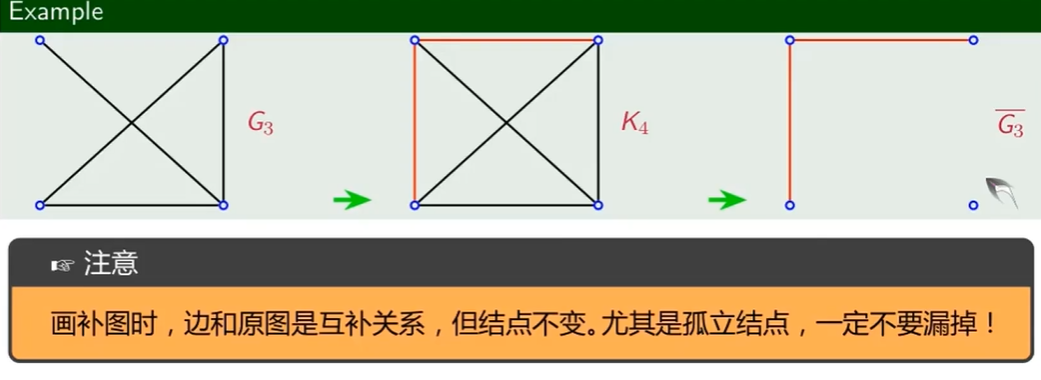
补图
将原图(G)从其完全图($K_n$)中删除对应的边,即为补图,记作$\overline{G}$。
- 邻接矩阵求补图的方法 - 除主对角线外,所有值取反
示例
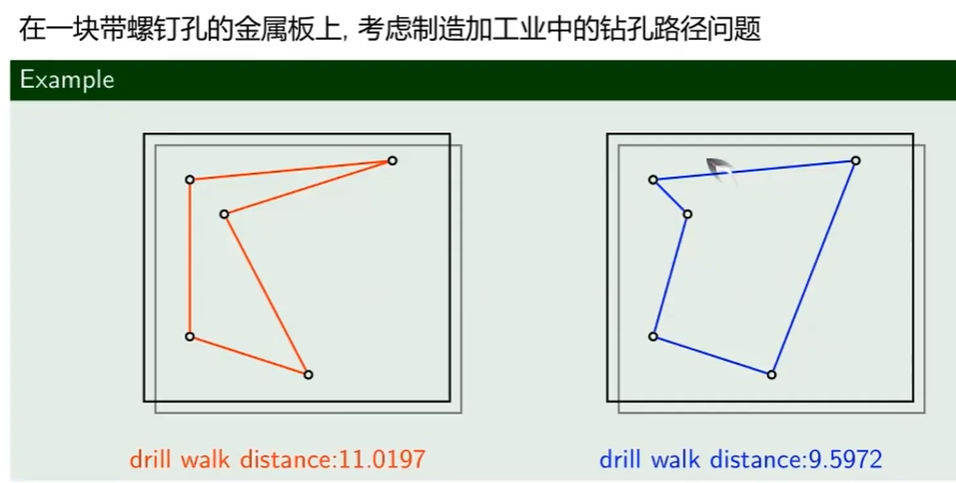
应用
握手定理
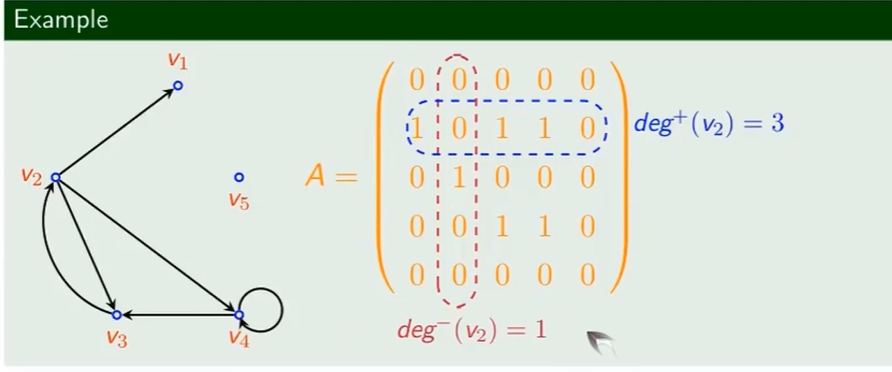
结点的度数
最[大\小][度\出度\入度]
邻接矩阵计算度数
示例
图论基本定理(握手定理)
示例:通过结点度数判断结点个数
无向图的结点度数和边数的关系
有向图的结点度数和边数的关系
度数序列
图的同构
困惑
- 为什么要研究图的同构
- 什么是图的同构
- 如何判定图的同构
回复
- 图的结构决定图的本质特征,结构相同的图会有类似的性质。
- 同构的定义
同构的定义
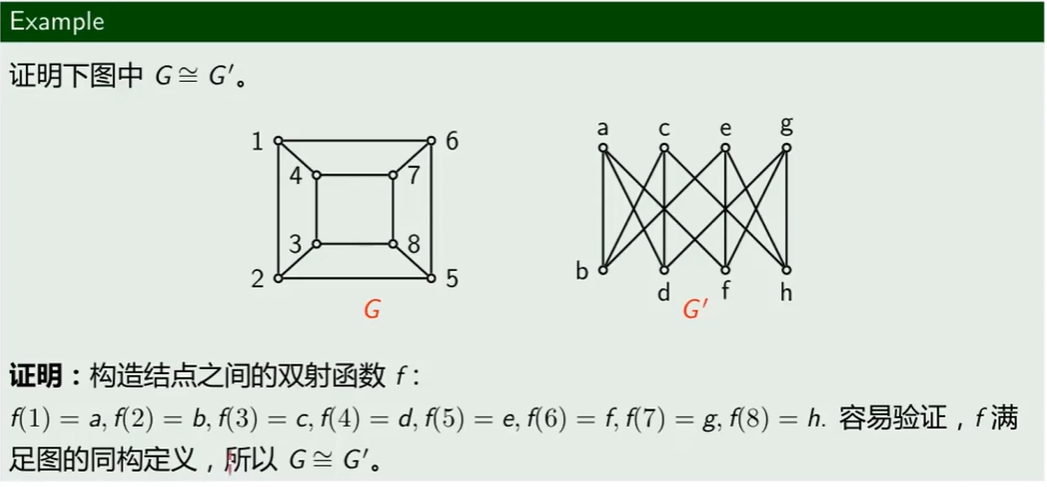
证明两个图同构
判断同构
结点少的时候
- 结点度数
- 结点邻接点 情况
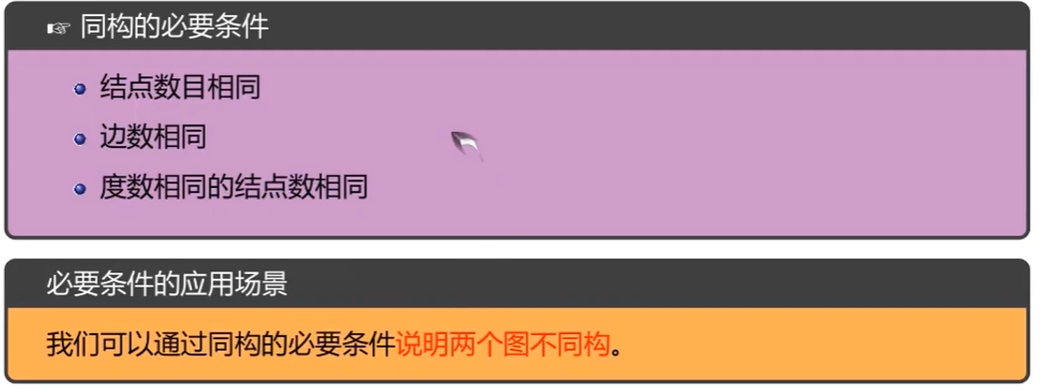
必要条件
注意:满足必要条件不一定是同构,但同构一定满足必要条件。
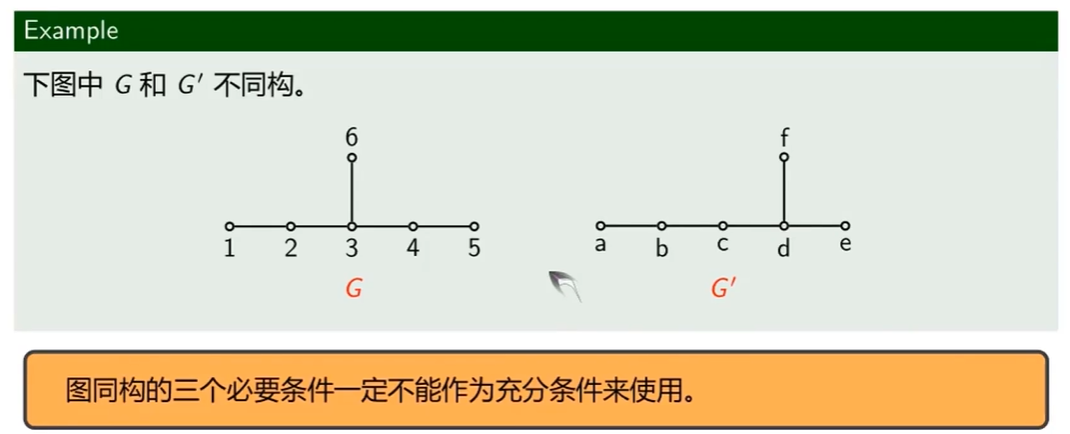
用于判断两个图是否不同构
反例示例
通路和回路
问:
- 为什么会有通路和回路问题?
答:
概念定义
简单-复杂 通路
- 边均不同 -简单
- 反之 -复杂
基本/初级 通路
- 在简单图的基础上,结点均不相同
- 即,结点、边均不相同
- 回路允许起始和结尾的结点相同
$\Gamma$ - Gamma
举例
记号简化
- 用结点 或 边的序列来表示通路
通路数量
可以解决的问题:
矩阵计算的方法
- 这里限定为线图是为了简单起见
- 由于邻接矩阵是基于线图定义的
- 考虑非线图情况,需要对邻接矩阵定义做扩展
问:
- 矩阵乘法的计算方法有哪些?
- 矩阵的幂次为什么能代表结点步数的可达性?
答:
1. 答:
1. 标准定义法(按行 × 按列)–内积
最常见的矩阵乘法定义:
$设 A=(a_{ij}) 是 m\times n 矩阵,B=(b_{ij}) 是 n\times p 矩阵,则:$
$C = A \cdot B, \quad C=(c_{ij}), \quad c_{ij} = \sum_{k=1}^{n} a_{ik} b_{kj}.$
👉 计算时就是:取 A 的第 i 行,与 B 的第 j 列做点积。
2. 按行分块法
把矩阵分成行向量和列向量。
例如:
$A = \begin{bmatrix} \vec{r}_1 \ \vec{r}_2 \ \vdots \ \vec{r}_m \end{bmatrix}, \quad B = \begin{bmatrix} \vec{c}_1 & \vec{c}_2 & \cdots & \vec{c}_p \end{bmatrix}.$
- 那么 $c_{ij} = \vec{r}_i \cdot \vec{c}_j$ (点积)。
这种写法直观,常用于人工演算。
3. 分块矩阵乘法
如果矩阵很大,可以把它们分成小块再相乘
👉 好处:分治计算,可以并行化,也方便在编程里实现。
4. 逐元素展开法(列向量组合)
把矩阵 B 看成一列列向量:
$B = \begin{bmatrix} \vec{b}_1 & \vec{b}_2 & \dots & \vec{b}_p \end{bmatrix},$
那么:
$AB = \begin{bmatrix} A\vec{b}_1 & A\vec{b}_2 & \dots & A\vec{b}_p \end{bmatrix}.$
👉 即矩阵乘法就是对 BBB 的每一列单独做一次线性变换。
5. 算法角度
(1) 朴素算法
复杂度:$\mathcal{O}(n^3)$。
常用于小矩阵或教学。
(2) Strassen 算法
通过减少乘法次数,复杂度降到 $\mathcal{O}(n^{2.81})$。
适合大矩阵,但在小规模时不划算。
(3) Coppersmith–Winograd 算法及改进
目前最优复杂度约 $\mathcal{O}(n^{2.3728596})$。
主要用于理论研究,大规模实际运算仍依赖优化库(如 BLAS、GPU)。
(4) 稀疏矩阵乘法
如果矩阵稀疏,可以只计算非零元素,复杂度与非零元素数量相关,远优于 $\mathcal{O}(n^3)$。
6. 在离散数学/图论里的用法
邻接矩阵幂:利用矩阵乘法计算步数。
布尔矩阵乘法:若只关心“是否存在路径”,用逻辑运算代替加法和乘法:
$c_{ij} = \bigvee_{k=1}^n (a_{ik} \wedge b_{kj}).$
(即存在至少一条路径即可,常用于传递闭包/可达性问题)。
2. 答:
1. 邻接矩阵与可达性
设有一个有向图 $G=(V,E)$,其中顶点数 $∣V∣=n$。
定义图的邻接矩阵 $A=(a_{ij})$:
$a_{ij} = \begin{cases} 1 & \text{如果存在边 } i \to j \ 0 & \text{否则} \end{cases}$
这样,矩阵 A 就把图的结构编码了进去。
2. 矩阵乘法与一步路径
矩阵乘法的定义:
$(A^2){ij} = \sum{k=1}^n a_{ik} a_{kj}$
$a_{ik}=1$ 表示 从 i 能走到 k(一步)
$a_{kj}=1$ 表示 从 k 能走到 j(一步)
所以 $a_{ik}a_{kj}=1$ 就表示:存在一个中间点 k,使得 从 i 到 j 能走两步。
把所有可能的 k 加起来,就是 从 i 到 j 的所有两步路径的条数。
于是:
$(A^2)_{ij} = \text{从顶点 (i) 到顶点 (j) 的所有长度为 2 的路径数}$
3. 推广到多步
同理:
$(A^m)_{ij} = \text{从顶点 (i) 到顶点 (j) 的所有长度为 (m) 的路径数}$
因此:
A 本身告诉你“一步可达性”;
$A^2$ 告诉你“两步可达性”;
$A^m$ 告诉你“走 mmm 步的可达性”。
4. 从路径数到可达性
如果我们只关心“能不能到达”,而不是“有多少条路径”,只需把所有非零元素视为 1:
$\text{可达性矩阵}(m) = \begin{cases} 1 & \text{如果 } (A^m)_{ij} > 0 \ 0 & \text{否则} \end{cases}$
5. 直观理解
矩阵乘法其实就是组合可能的中间点:
$(AB)_{ij}$ 的求法就是“枚举所有中间点 k”;
这和“从 i 走到 j,经过某个中间点 k”完全对应;
因此矩阵的幂就自然代表了“走若干步”的可能性。
通路数量的计算
归纳法证明
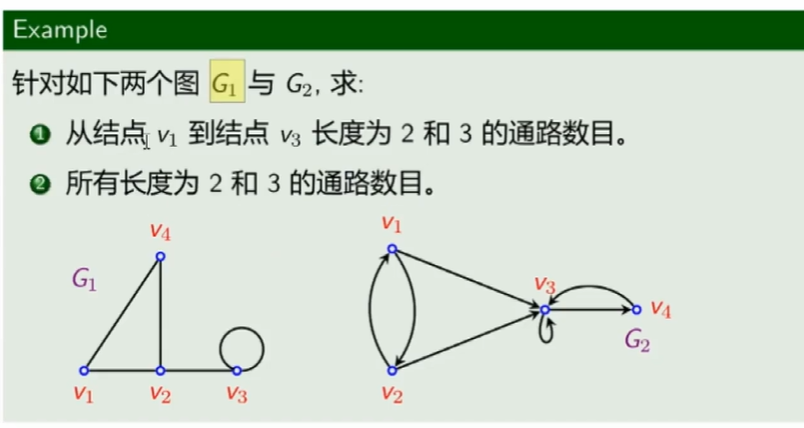
例题
解G1
解G2
拓展题
可达性与最短通路
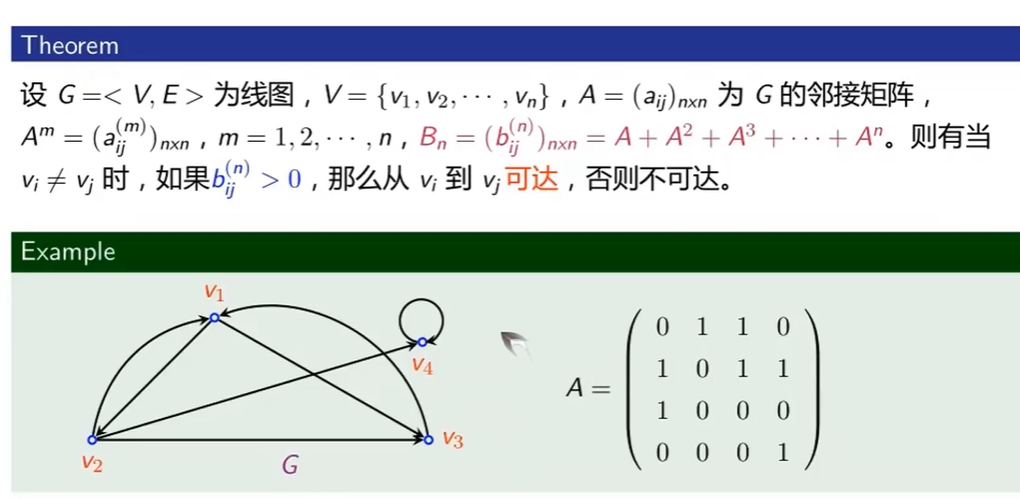
可达关系判定引理
可达关系的判定定理
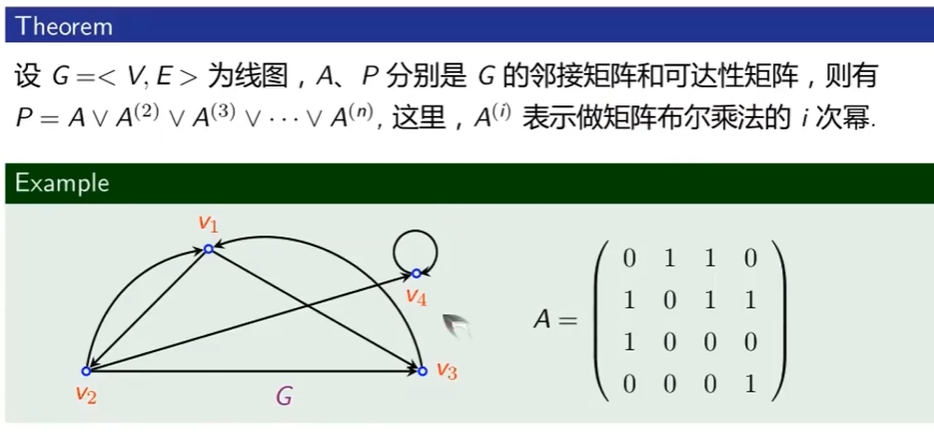
可达性矩阵
- 采用布尔运算
应用布尔运算求解
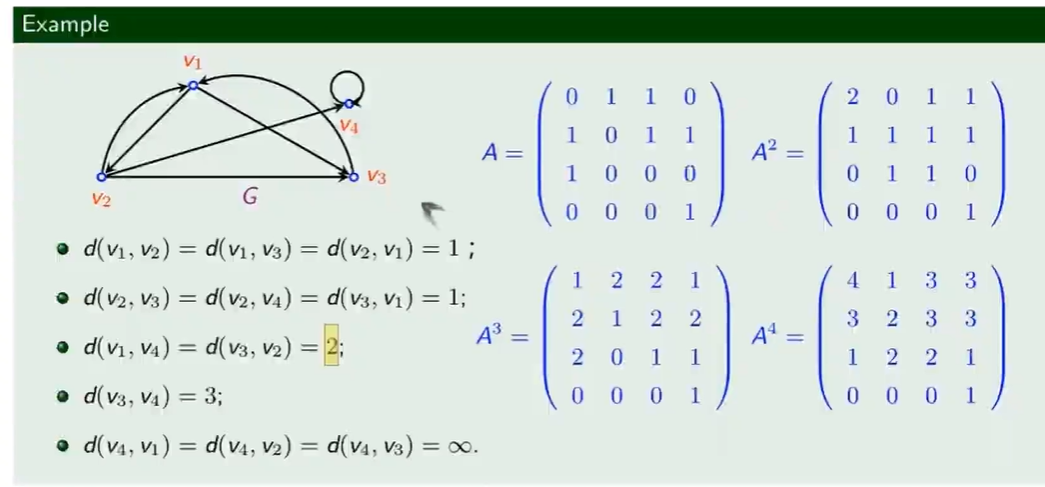
短程线及其距离
- 最短通路 - 短程线
- 最短通路长度 - 距离 $d(v_i,v_j)$