离散小记
离散数学
思维导图
命题与范式
1. 一切的开始:从“砖头”到“句子”
- 命题变元 (Propositional Variable):这就是最最基础的“原子”或者说“砖头”,比如
p、q。它本身代表一个非真即假的简单陈述。 - 文字 (Literal):这个概念很重要。你给的词里有“短语”,但在标准逻辑里,我们通常叫它“文字”。它就是一个变元或者这个变元的“否定”,比如
p和¬p。你可以把它想象成带正电(p)和带负电(¬p)的砖头,比单个的砖头多了一点信息。 - 命-题公式 (Propositional Formula):把这些“文字”用“合取 (∧, AND)”和“析取 (∨, OR)”这些逻辑胶水粘起来,就成了一个完整的“句子”,也就是命题公式。它是我们整个故事的主角。
2. 分析主角的工具:真值表
- 真值表技术 (Truth Table):这玩意儿就是个“照妖镜”。无论一个公式多复杂,把它扔进真值表,它在所有可能性(所有变元的真假组合)下的结果是真是假,都一目了然。这是我们后面所有操作的基础。
3. 两条主线:析取范式 (DNF) 与 合取范式 (CNF)
现在,故事分成两条线了,就像一个公式可以有两种不同的“标准照”。
路线一:析取范式(DNF)—— 找“真”
- 极小项 (Minterm):你看真值表里,那些让整个公式结果为 真 (True) 的行。每一行都对应一个“极小项”。极小项是个“合取”式,包含了所有变量,并且能精确匹配那一行的真假赋值。比如
(p=0, q=1)对应的极小项就是¬p ∧ q。它就像是某个案件中,能让“真相大白”的唯一一种关键线索组合。 - 主析取范式 (PDNF):把所有能让公式为“真”的极小项,用“析取 (∨)”连起来,就成了主析取范式。因为它是由所有“真”的情况构成的,所以它和原公式是等价的。这是公式的第一个“标准身份证”,全球唯一。
- 析取范式 (DNF):PDNF是一种要求很严格的DNF。普通的DNF没那么严格,只要整体结构是“合取式的析取”,比如
(p) ∨ (¬p ∧ q),就算。
路线二:合取范式(CNF)—— 排除“假”
- 子句 (Clause):这是CNF的基本单元,它本身是一个“析取”式,比如
(p ∨ ¬q)。 - 极大项 (Maxterm):对应地,你看真值表里那些让公式结果为 假 (False) 的行。每一行都对应一个“极大项”。极大项是个“析取”式,它也包含了所有变量,并且它的值在那一行恰好为假。比如
(p=0, q=1)对应的极大项是p ∨ ¬q。它就像是案件中,必须被排除的一种“错误可能性”。 - 主合取范式 (PCNF):把所有能让公式为“假”的极大项,用“合取 (∧)”连起来,就成了主合取范式。它的逻辑是“不能是这种情况,并且也不能是那种情况……”,通过排除所有错误,剩下的自然就是正确的。这是公式的第二个“标准身份证”,同样全球唯一。
- 合取范式 (CNF):PCNF是严格版的CNF。普通的CNF只要结构是“析取式的合取”(也就是一堆子句的合取)就行。
4. 补充说明
- 编码 (Encoding):这很好理解。就是给变元的真假赋值(比如 p=T, q=F)一个二进制编号(10)。这个编号
i正好对应极小项mᵢ和极大项Mᵢ的下标,让找它们变得非常方便。 - 总结一下:任何一个命题公式,都能被唯一地表示成它的主析取范式(所有“真”的可能性的总和)和主合取范式(排除所有“假”的可能性的结果)。而真值表,就是找到这些“真”和“假”的可能性的核心方法。
命题
联结词
优先级
\(\lnot\ >\ \land\ >\ \lor\ >\ \to\ >\ \leftrightarrow\)

基本等价关系
逻辑电路简化
并联:$\lor$
串联:$\land$
\((\lnot G\lor H)\land(\lnot H\lor G)\) —
公式
个体词、谓词与量词
引入
表示
个体词
谓词
命题可以表示成0元谓词,但 0元谓词 不等于 命题,当0元谓词中的谓词为谓词常量时,才成为命题。
量词
符号化
规则
谓词公式
解释
分类
可判定性
公式等价
前束范式
求解步骤
求解示例
推理
推理定律-基本蕴含关系
推理规则-量词消去与添加 US|UG|ES|EG
全称特指规则-消去
全称推广规则-添加
存在特指规则-消去
存在推广规则-添加
谓词综合推理
xx是xx,符号化时,全称量词用 蕴含$\rightarrow$,存在量词用 合取$\land$
谓词演绎举例
实例代入的顺序
反证法
应用
关系理论
序偶与笛卡儿积
序偶(有序组)
笛卡儿积定义
笛卡儿积性质
- 不满足 结合律、交换律
- 对交、并运算,满足分配律
笛卡儿积推广
二元关系
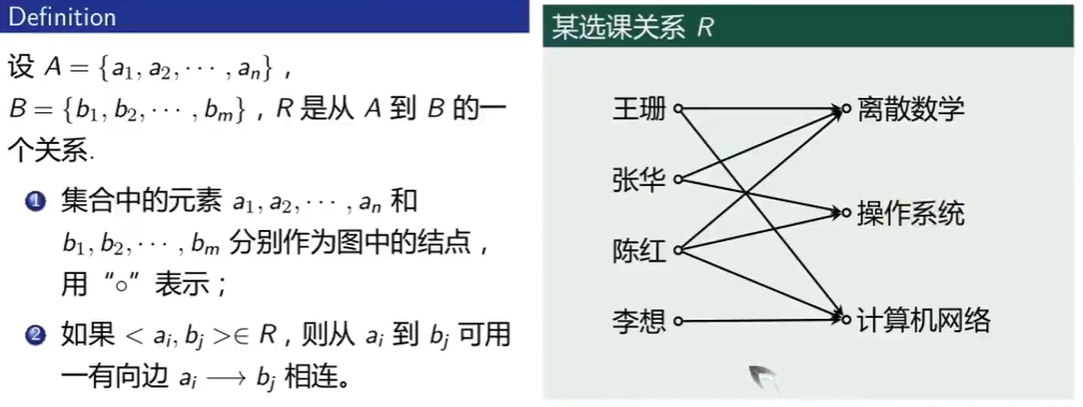
二元关系定义
所有的多元关系都可以写成二元关系
二元关系符号表示
集合表示(枚举与叙述)
关系枚举
图形表示
关系矩阵表示
布尔矩阵的运算
并和交运算
积运算
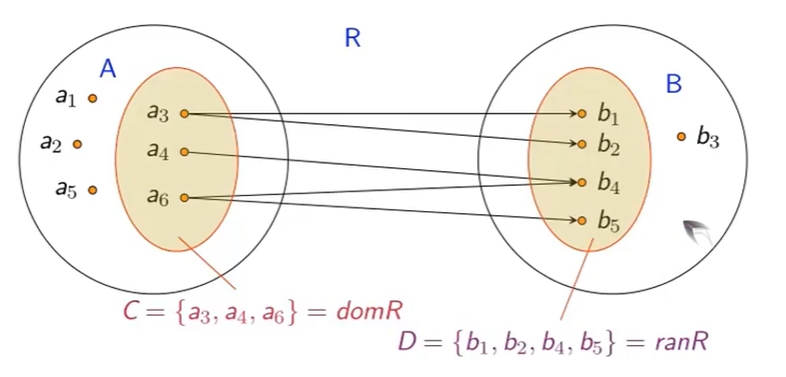
定义域与值域
关系运算
并交差补
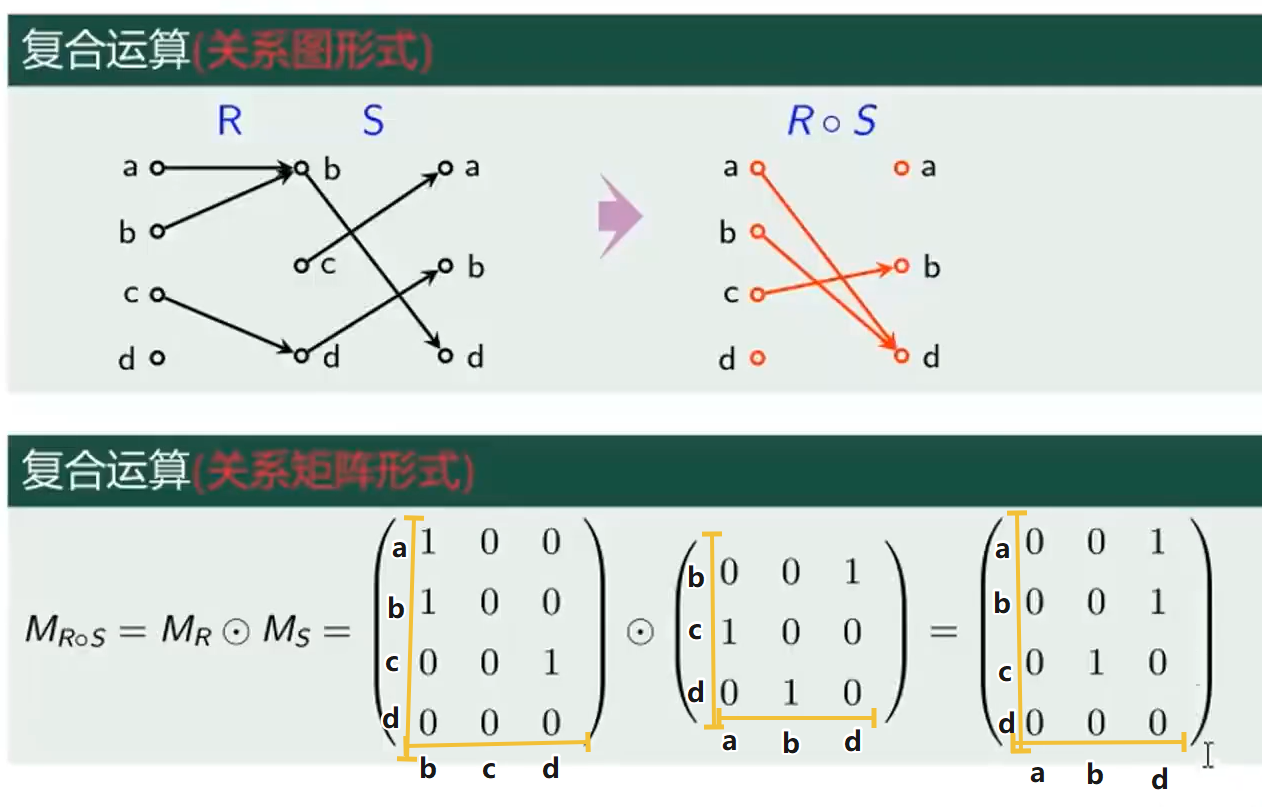
复合运算(关系矩阵-布尔积)
技巧:A有n条路,B有m条路,C有k条路,A与B直连,B与C直连
A与B的连通情况为$n\times m$ 矩阵 $M_R$
B与C的连通情况为$m\times k$ 矩阵 $M_S$
A与C的连通情况为$n\times k$ 矩阵 $M_{R\circ S}=M_R\bigodot M_S$
说明:仅拿第一列举例
$M_R$为a、b、c、d 到 b、c、d的连通关系矩阵
- b列向量,分量 分别代表 a/b/c/d连通b情况
$M_S$为b、c、d 到 a、b、d的连通关系矩阵
- a列向量,分量 分别代表 b/c/d连通a的情况
$M_R\bigodot M_S$ 进行矩阵乘积,a列向量进行矩阵变换
每个分量分别变换成$M_R$中的 b、c、d 列向量,这些列向量的和为a列向量变换后的结果
等同于 a到 b、c、d的连通性,再到a、b、c、d的连通性,0为不通,1为通。
复合运算定律及证明
分配律
@startuml
left to right direction
actor A as a
rectangle B {
node b1
node b2
}
actor C as c
a --> b1 : R
a --> b2 : R
b1 --> c : S1
b2 --> c : S2
note right of c
(R∘S1) = {<a,c>} via b1
(R∘S2) = {<a,c>} via b2
(R∘S1) ∩ (R∘S2) = {<a,c>}
但:
S1 ∩ S2 = ∅
R∘(S1∩S2) = ∅
end note
@enduml
逆运算
逆运算定律
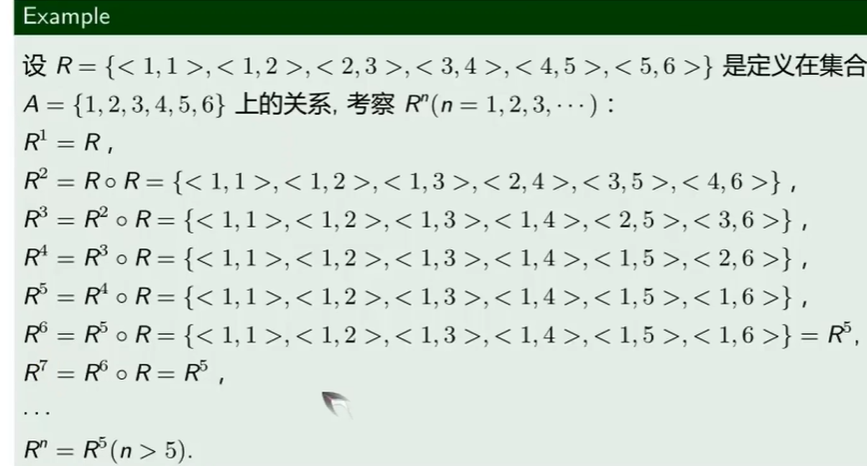
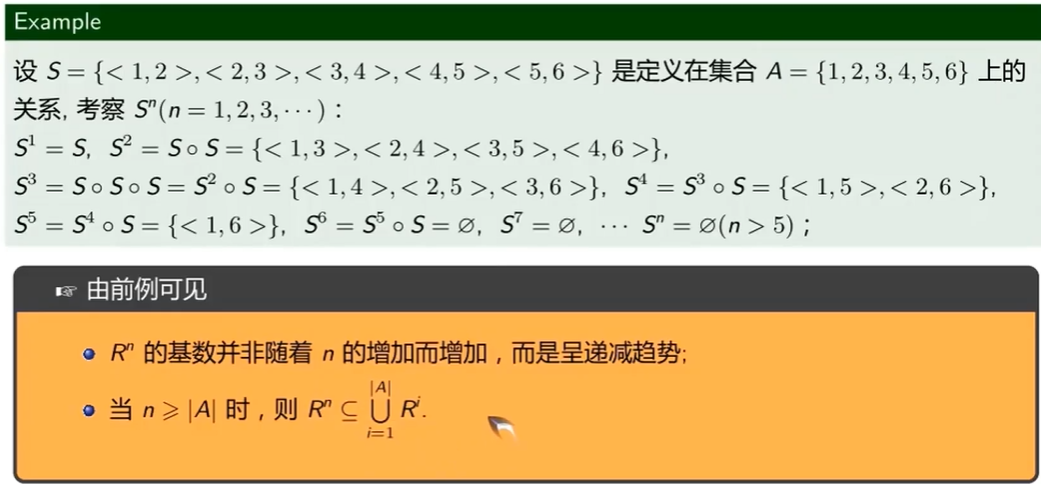
幂运算
$R^n\in \bigcup_{i=1}^{|A|}R^i$
i从1到A的基数$R^i$的并
- 当R是定义在 集合A上的关系时
R从 A 次幂开始,就不会产生新的序偶了
收敛性
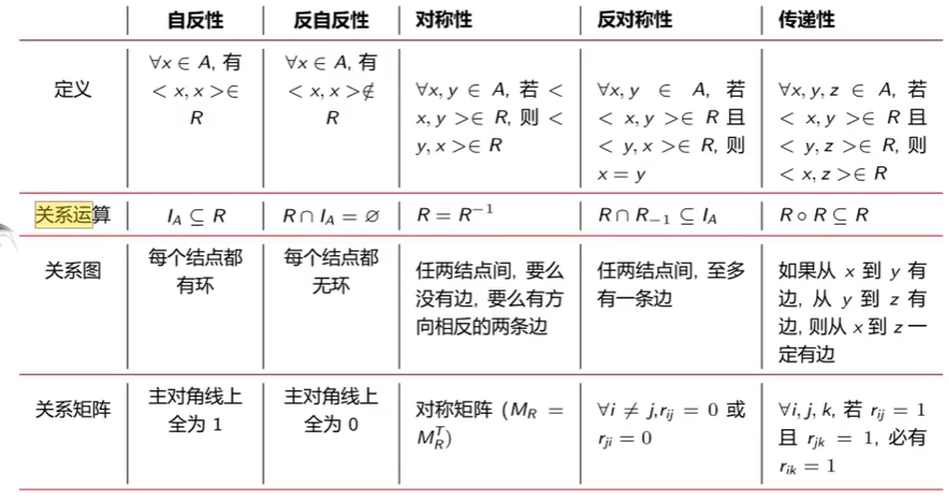
关系的性质
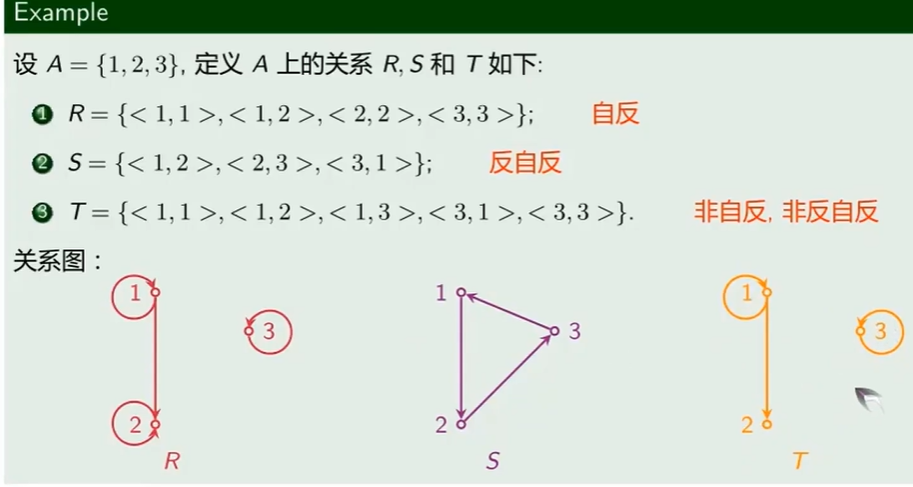
自反性与反自反性
- 自反性:对任意的 $x\in A$ ,x与自身相关
- 反自反性:x与自身不相关
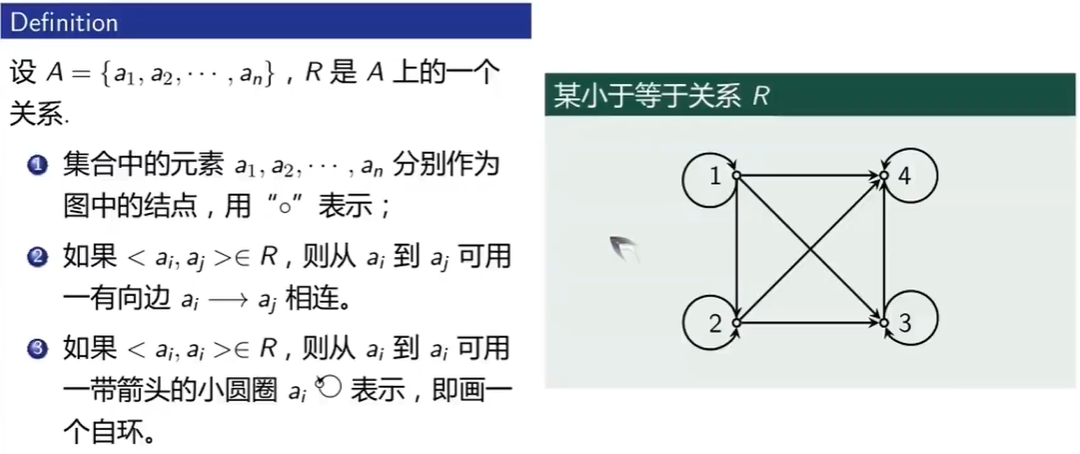
关系图
矩阵
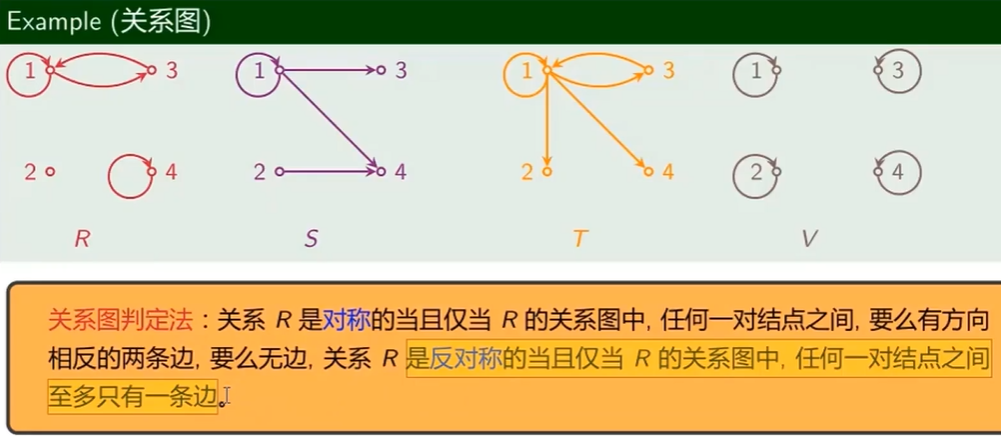
对称性与反对称性
- 非对称、非反对称:既存在 对称的关系、又存在反对称的关系
关系图
- 对称关系:两节点的边是双向的、或无边
- 反对称关系:只存在单向边、或无边
- 非反对称、非对称关系:既存在双向边、又存在单向边
- 对称、反对称关系:只有自环
矩阵
- 对称:关于主对角线对称,值相同
- 反对称:关于主对角线,不存在相同值
- 既对称又反对称:主对角线上,值全为1
传递性
注意点:定义是$<x,y>\in R\ \land\ <y,x>\in \ R\ \rightarrow\ <x,z>\in R$
前件不满足时,公式为真
S={<1,2>}; 前件未满足,也具有传递性
关系图
矩阵
- 节点对应的是 行值、列值
- 序偶<x, y> 则对应矩阵上的具体值
- 则有:传递关系$(r_{ij}=1)\land (r_{jk}=1)\rightarrow (r_{ik}=1)$
判定定理
总结判定方法
性质的判定
注意:对称、传递均是蕴含关系
相关证明
关系性质的保守性
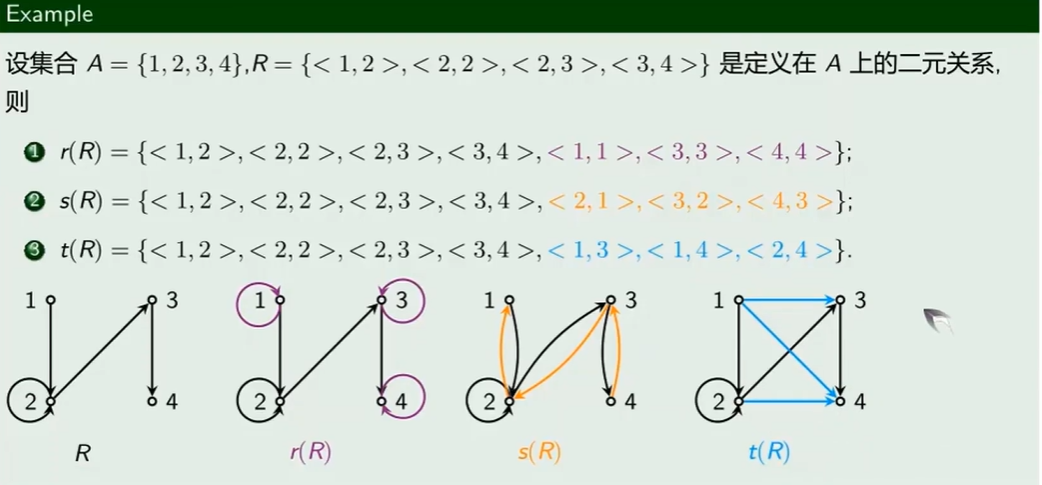
关系闭包
闭包思想
闭包定义
闭包关系图
闭包求解
等价关系
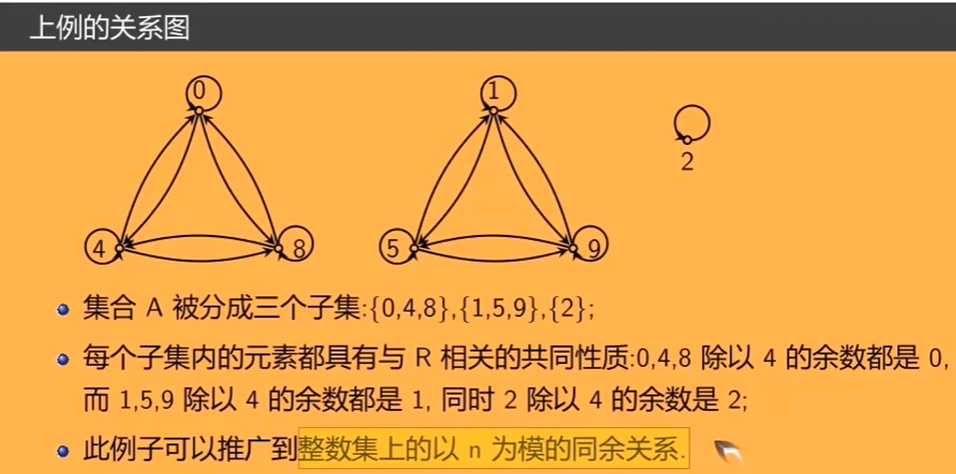
定义
例子与推广
等价类
引入
定义
3条性质与证明
商集
计算商集的通用过程
等价类的应用场景
- 报文转发
- 软件黑盒测试
- 数据挖掘
- 霍兰德分析
集合的划分
等价划分
划分导出的等价关系
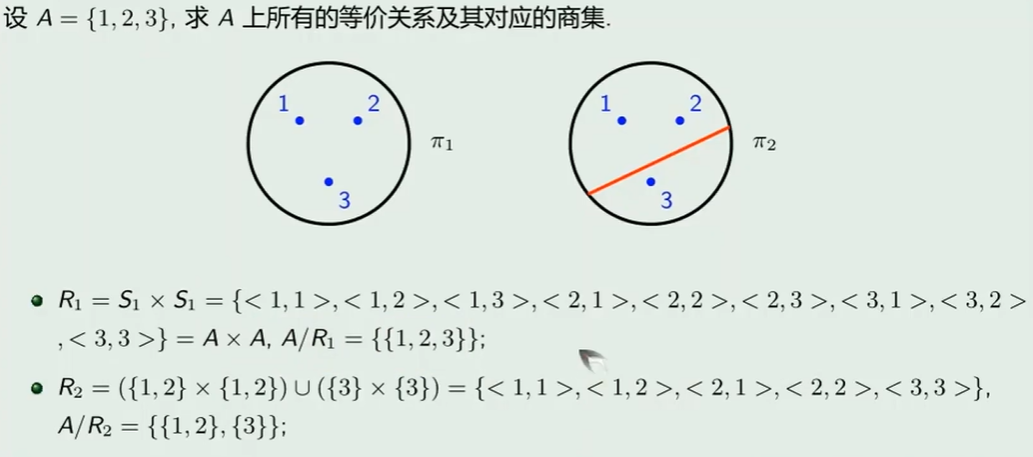
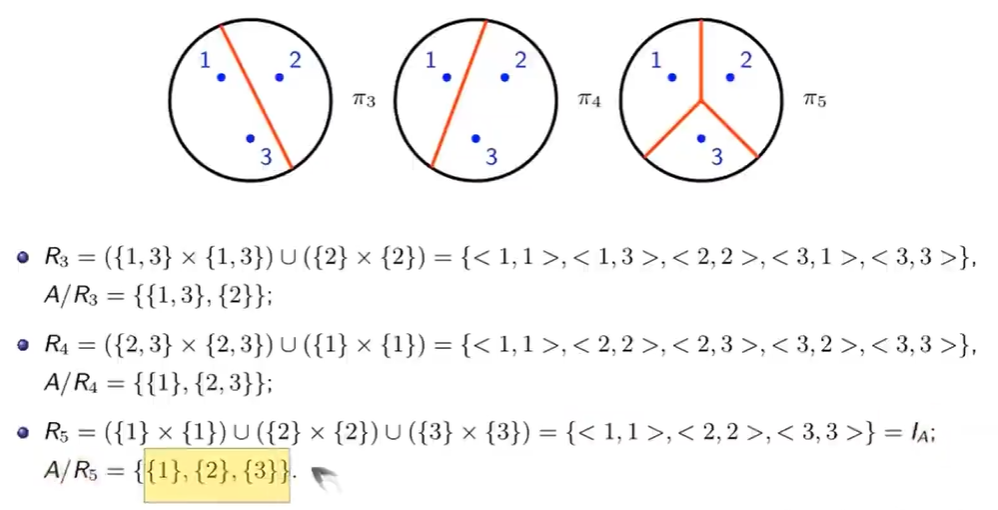
集合的所有等价关系及商集
- A = {1, 2, 3} 共有 2 的 9 次幂种关系 ?
解释:
你的集合:A = {1, 2, 3},咱们就把它想象成三个人:张三、李四、王五。
- “关系”是啥? 就是这三个人之间可不可能存在单向的箭头。
- 比如,张三 → 李四 (可以表示“张三认识李四”)
- 张三 → 张三 (可以表示“张三认识他自己”)
- 总共有多少种可能的箭头?
- 张三可以指向3个人(他自己、李四、王五)
- 李四可以指向3个人
- 王五可以指向3个人
- 所以,总共有 3 × 3 = 9 种可能的箭头。
- 2的9次幂是怎么来的? 对于这9种可能的箭头,每一种都只有两种状态:“存在”或“不存在”。
这就好比有9个开关,每个开关都可以选择开或关。总共的组合数就是 2 × 2 × … (9个2相乘) = 2⁹ = 512。
所以,2的9次幂指的是:在{1, 2, 3}这三个人之间,你能定义出来的所有乱七八糟、毫无规律的“关系”的总数。比如“1认识2,2不认识1,3认识3……”这种。
- 到底有多少种“等价关系”(分帮派)?
解释:
满足上面三大帮规的关系,其实就是在做一件事:把这三个人分成不同的小团体(非空、不相交)。这在数学上就叫“划分” (Partition)。
对于张三、李四、王五这三个人,咱们有几种分法?
- 大家全在一个帮派里:
- { {张三, 李四, 王五} }
- 这是一种分法。
- 分成两个帮派(一个两人帮,一个独行侠):
- { {张三, 李四}, {王五} }
- { {张三, 王五}, {李四} }
- { {李四, 王五}, {张三} }
- 这有三种分法。
- 三个人各自为政,都当独行侠:
- { {张三}, {李四}, {王五} }
- 这是一种分法。
总共加起来:1 + 3 + 1 = 5 种。
偏序关系与偏序集
字典排序与证明
偏序关系证明
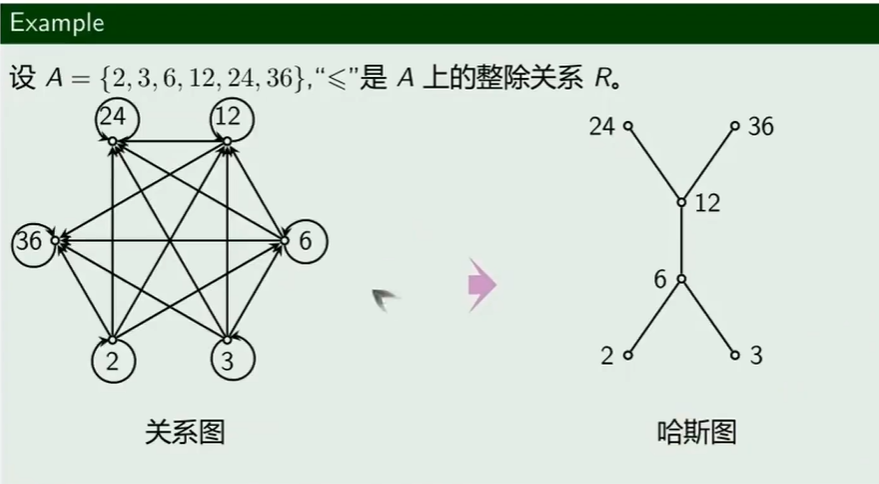
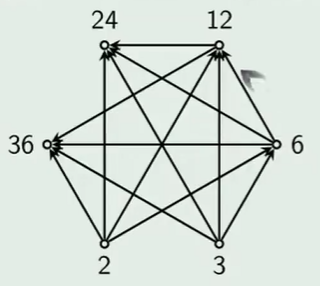
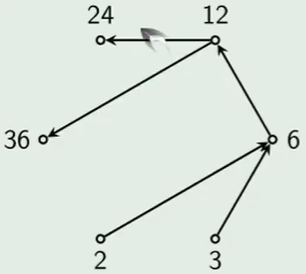
哈斯图
哈斯图引入
哈斯图定义
哈斯图画法
特殊元素
- 最大元元需要全都可比
- 极大元允许存在不可比
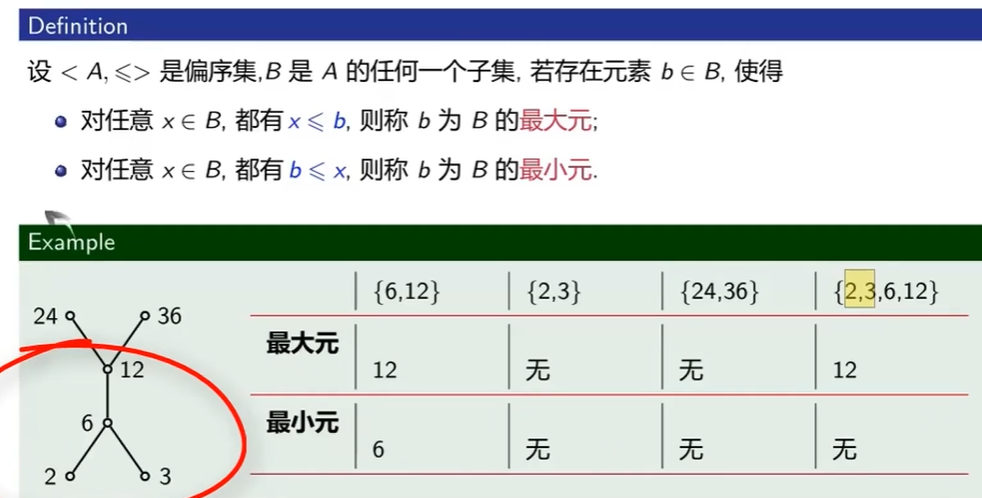
- 最小元不允许存在同级不可比
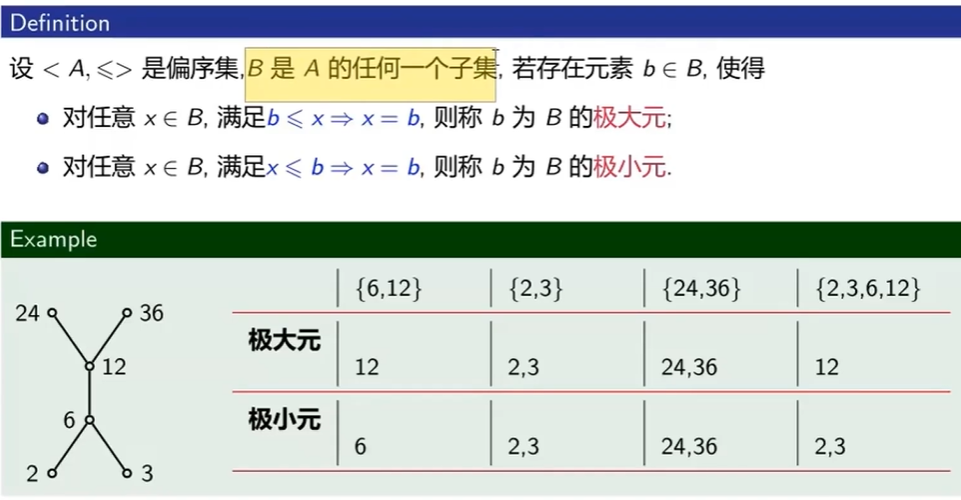
- 极小元允许存在不可比
- 上、下界对子集内元素均可比
- 上、下界允许存在同级不可比
- 上、下确界不允许存在同级不可比
最大元和最小元
极大元和极小元
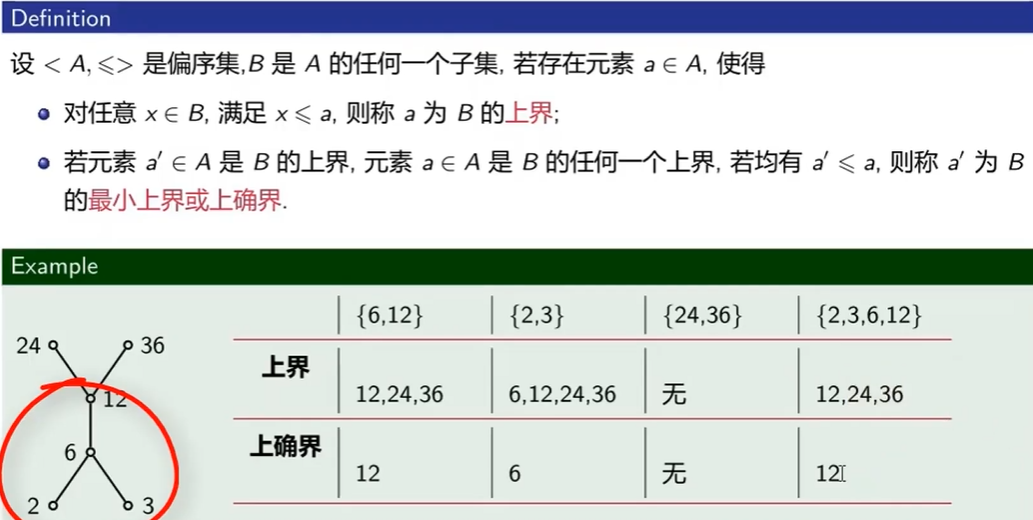
上界与上确界
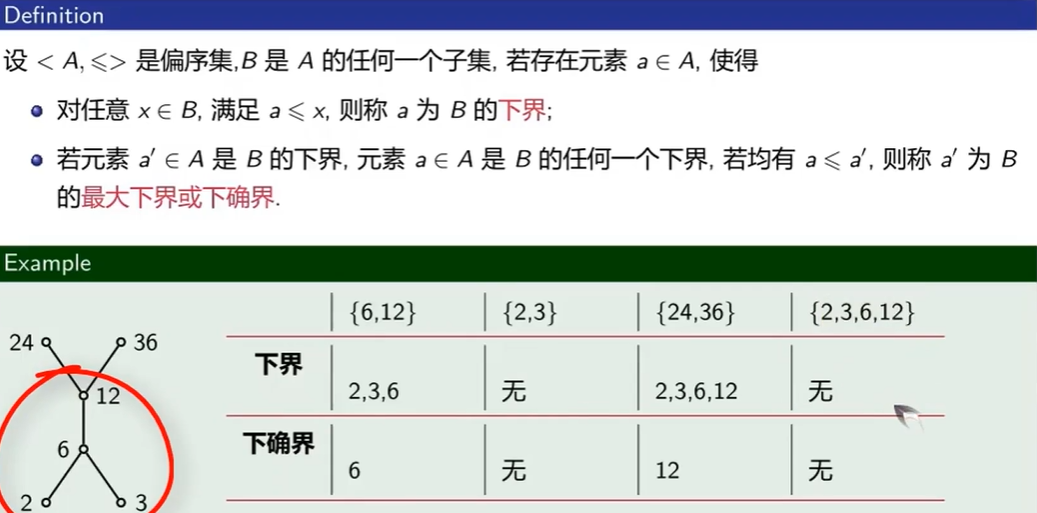
下界与下确界
其它次序关系
拟序关系
- 反自反
- 传递
- 反对称
- 反自反+传递$\implies$反对称
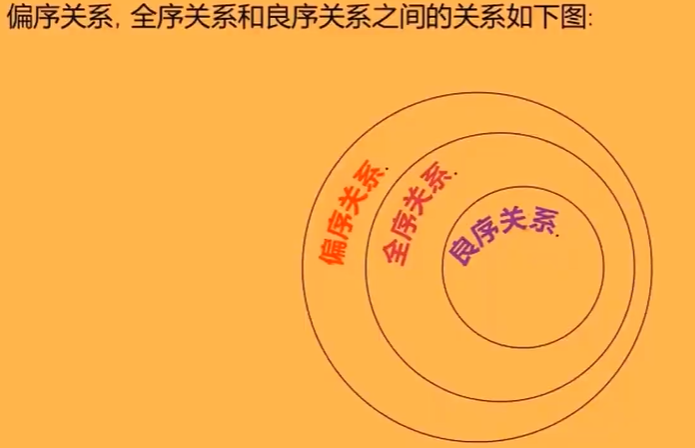
全序关系
- 全序关系是偏序关系全可比的版本
- 幂集:一个集合的所有子集(包括空集和它自己)所构成的集合。 表示符号为 P(A)
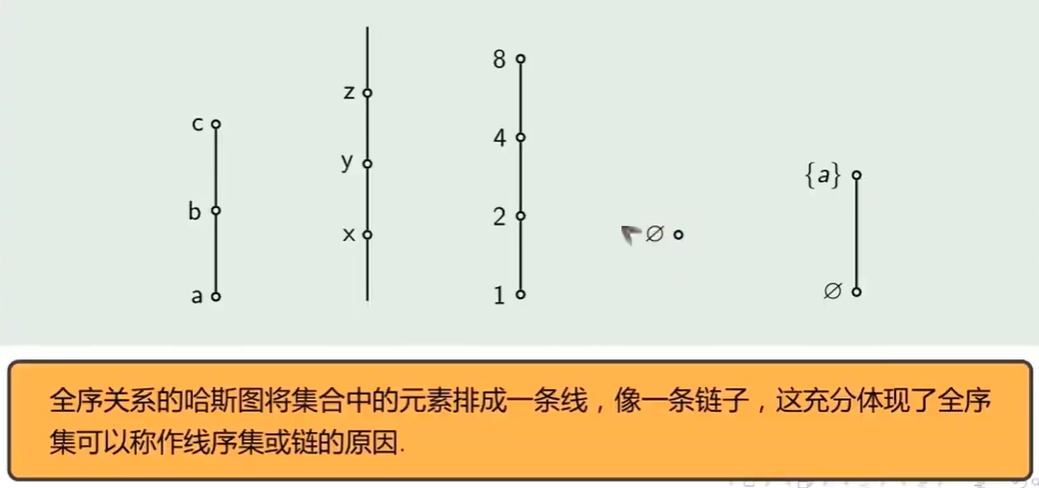
全序关系的哈斯图
良序关系
咱们把这个规则拆成两条,就更清楚了:
规则1:必须是“全序关系” (Total Order)。
- 啥意思? 就是队伍里任何两个人拎出来,都得能比个高下,分出谁前谁后。不允许出现“咱俩谁也不服谁,没法比较”的情况。
- 生活比喻: 就是一条单行线,所有人都在线上,没有分叉。你我之间,要么你在我前面,要么我在你前面,不存在第三种可能。
- 数学语言: 对于集合A中任意两个元素
a和b,要么a ≤ b,要么b ≤ a,必须得占一样。
规则2:【核心灵魂】任何“非空子集”都必须有“最小元素”。
- 啥意思? 这就是“带头大哥”规则。从这条队伍里,不管你怎么捞人(只要你不是一个人都不捞),你捞出来的这群人里,一定有一个人是他们中排在最最前面的。
- 生活比喻: 想象一队长长的队伍。
- 我从中间随便圈出10个人,这10个人里一定有1个是排在最前面的。
- 我从队尾圈出5个人,这5个人里也一定有1个是排在最前面的。
- 甚至我把整个队伍都圈起来,也必须有一个人是全队的“排头兵”。
- 关键点: 这个规则杜绝了“无限往下”的可能性。你永远能找到一个“底”。
总结一下:良序关系 = 全序关系 + 任何子集都有“排头兵”。
良序定理
定义即:声明 任何集合都可以被良序化的断言。
- 争论:良序定理与选择公理是等价的
- 良序定理与数学归纳法、超限归纳法的关系?
解答:
想象一下,我们要证明“这座无限高的楼梯,每一阶都是牢固的”。
Part 1: 三种证明工具,三种思路
- 数学归纳法 (PMI): 最经典的“一步一步爬”
- 它的逻辑是:
- 第一步 (Base Case): 我先亲自踩一下第0阶楼梯,确认它是牢固的。
- 第二步 (Inductive Step): 我再证明一个“传递规则”:如果我站的第k阶是牢固的,那么我往上迈一步到的第k+1阶也必然是牢固的。
- 结论: 既然第0阶牢固,那根据规则,第1阶就牢固;既然第1阶牢固,那第2阶就牢固……以此类推,每一阶都牢固!
- 小Z点评: 这是我们最熟悉的工具,像多米诺骨牌一样,一个推一个。它的特点是向前看,从已知推未知。它只适用于像自然数
0, 1, 2, 3,...这样可以一阶一阶往下数的集合。
- 良序定理 (WOP): “抓出第一个烂台阶”
- 它的逻辑是:
- 这是一个声明而不是一个过程:“对于自然数(楼梯的阶数)的任何一个非空集合,里面必然存在一个最小的数”。
- 换成楼梯的场景就是:“如果这座楼梯存在‘不牢固’的台阶,那么把所有‘不牢固’的台阶编号收集起来,必然能找到一个编号最小的、也就是第一个不牢固的台阶。”
- 如何用它来证明? (反证法):
- 假设“并非所有台阶都牢固”。
- 根据良序定理,必然存在第一个不牢固的台阶,我们叫它第m阶。
- 因为它是第一个不牢固的,那意味着它前面的所有台阶,从第0阶到第m-1阶,全都是牢固的。
- 等等!如果我们之前证明了归纳法里的那个“传递规则”(即“如果k阶牢固,则k+1阶也牢固”),那么既然第m-1阶是牢固的,第m阶就必定是牢固的啊!
- 这就产生了矛盾!我们假设第m阶不牢固,但又推导出它必须牢固。
- 结论: 矛盾的根源在于最初的假设。所以假设不成立,所有台阶都是牢固的。
- 小Z点评: 这是向后看的逻辑。它不关心怎么一步步构建,而是通过“抓坏人”来证明没坏人。它关注的是存在性(一定有个最小的)。
- 超限归纳法 (Transfinite Induction): “升级版”的爬楼梯
- 它要解决什么问题?: 普通的数学归纳法只能爬一阶一阶的楼梯。但如果楼梯长得特别诡异呢?比如,爬了无数阶(0, 1, 2, 3…)之后,突然出现一个“平台”,这个平台本身也是一阶,但它没有“前一阶”(比如第ω阶,ω是最小的无穷序数)。你怎么爬到这个“平台”上?
- 它的逻辑是 (三步):
- 第0阶是牢固的。(和PMI一样)
- 后继阶 (Successor Step): 如果第α阶是牢固的,那么它的下一阶“α+1”阶也是牢固的。(和PMI一样)
- 极限阶 (Limit Step) - 这是关键!: 对于一个没有“前一阶”的“平台”λ (比如第ω阶),如果它下面的所有台阶(0, 1, 2, …)都是牢固的,那么这个平台λ本身也必须是牢固的。
- 小Z点评: 这是数学归纳法的超级威力加强版。它不仅能处理一步一步走的情况,还能处理“飞跃”到某个极限点的情况。它适用于任何“良序集”,而不仅仅是自然数。
Part 2: 它们之间的关系
好了,了解了这三个工具的思路,我们来总结它们的关系:
- 良序定理 ↔️ 数学归纳法 (在自然数领域)
在离散数学我们最常接触的自然数集 N = {0, 1, 2, ...} 上,良序定理和数学归纳法是逻辑上等价的! 你可以把它俩看成是同一个数学真理的两种不同表述。
- WOP ⇒ PMI: 这就是我们刚才用良序定理证明“所有台阶都牢固”的那个过程。通过反证法,假设归纳法不成立,然后利用WOP找到第一个反例,从而导出矛盾。
- PMI ⇒ WOP: 同样可以用反证法。假设WOP不成立(即存在一个没有最小元素的非空子集S),然后用归纳法可以证明所有自然数都不在S里,从而导出S是空的,产生矛盾。
划重点: 在离散数学里,你可以认为它俩是一回事,是证明关于自然数性质的一体两面。一个“向前构建”,一个“向后反驳”。
- 超限归纳法是数学归纳法的“泛化”
- 数学归纳法是超限归纳法在自然数集这个最简单的良序集上的一个特例。
- 超限归纳法把证明的范围,从“一排多米诺骨牌”扩展到了“结构更复杂、可能有无穷个断点的多米诺骨牌阵列”。
- 良序定理是超限归纳法的基础
- 超限归纳法之所以能用,其合法性的根基就是良序这个属性。
- 一个集合可以被良序化(即可以给它的元素排出一个满足WOP的顺序),是可以使用超限归纳法的前提。而在更深的集合论里,有一个著名的“良序定理”,它指出任何集合都可以被良序化(这个定理等价于选择公理)。
总结一下
| 工具 | 核心思想 | 适用对象 | 与其它工具的关系 |
|---|---|---|---|
| 数学归纳法 (PMI) | 一步推一步,像多米诺骨牌 | 自然数 N | 在 N 上与良序定理等价 |
| 良序定理 (WOP) | 任何非空子集,必有最小的那个 | 在 N 上是公理,可推广到良序集 | 在 N 上与数学归纳法等价,是超限归纳法的基础 |
| 超限归纳法 | 不仅能一步步走,还能处理“极限”点 | 任何良序集(比 N 大得多) | 是数学归纳法的通用、加强版 |
所以,在离散数学的范畴里,你主要跟 良序定理 (WOP) 和 数学归纳法 (PMI) 打交道,并且可以放心大胆地认为它俩是等价的、可以相互推导的。而超限归纳法,你可以把它理解为是数学家们为了在更广阔、更奇异的数学世界(比如集合论)里继续使用归纳思想而打造的“星际飞船”。
答疑
谓词演绎的实例代入顺序
问:关于谓词演绎的证明,为什么证法1是错误的,证法2是正确的:
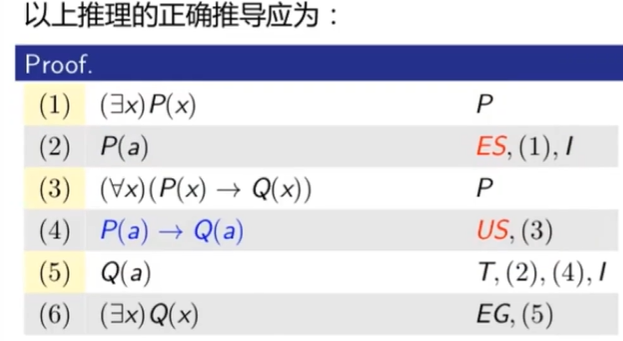
(∀x)(P(x) →Q(x)), (∃x)P(x) => (∃x)Q(x)
证法1
(1) (∀x)(P(x) →Q(x)) P
(2) P(a) →Q(a) US, (1), I
(3) (∃x)P(x) P
(4) P(a) ES, (3)
(5) Q(a) T, (2), (4), I
(6) (∃x)Q(x) EG, (5)
证法2
(1) (∃x)P(x) P
(2) P(a) ES, (1), I
(3) (∀x)(P(x) →Q(x)) P
(4) P(a) →Q(a) US, (3)
(5) Q(a) T, (2), (4), I
(6) (∃x)Q(x) EG, (5)
答:
这背后的关键,在于 EI (存在实例代入) 和 UI (全称实例代入) 这两个工具的“脾气”完全不同。
- UI (The Universal Adapter): 脾气超好,像个万能插头。因为
∀x意味着“对所有人都成立”,所以你可以把这个“所有人”的规则,应用到任何一个个体上,不管这个个体是老朋友(已经在证明里出现),还是新面孔。- EI (The Anonymous Suspect): 脾气古怪,限制极多。
∃x意味着“存在这么个家伙”,但我们不知道他是谁。所以,当你要把他拎出来讨论时,必须给他一个全新的、从未在案发现场(之前的证明步骤)出现过的代号。你不能随便指着一个已经在场的人说:“哦,那个‘存在的家伙’就是你!”
好了,记住这两个工具的脾气,我们来当一回福尔摩斯,分析一下这两个证法。
证法1:一个典型的“冤假错案”
咱们把这个证明过程翻译成一个破案故事:
- 前提1
(∀x)(P(x) →Q(x)): 福尔摩斯的铁律:“任何凶手(P)的口袋里,都有一张去往伦敦的火车票(Q)”。- 前提2
(∃x)P(x): 华生传来消息:“报告福尔摩斯,我们确认了,这屋子里肯定有一个凶手(P)!”
证法1的破案流程:
(∀x)(P(x) →Q(x))– (这是我们的铁律)(P(a) →Q(a))– (US/UI) 福尔摩斯随便指着房间里的一个人,比如管家a,然后说:“根据我的铁律,如果管家a是凶手,那他口袋里肯定有火车票。”
- 到这一步没问题。UI脾气好,可以应用到任何人身上。现在,“管家
a”这个名字已经出现在我们的案卷里了。(∃x)P(x)– (这是华生的情报)P(a)– (ES/EI) 灾难发生在这里! 警长冲了进来,听到福尔摩斯提到了“管家a”,又听到华生说“有凶手”,于是他想当然地一把抓住管家a,大喊:“凶手找到了!就是你,管家a!”
这错在哪?
错就错在,警长把“存在一个凶手”这个模糊的信息,强行安在了福尔摩斯刚刚随便提到的“管家
a”身上。EI规则要求你引入一个新面孔。如果非要用EI,你应该说:“我们把那个未知的凶手称为嫌疑人X (P(X))”,而不是直接认定为管家a。你把一个“存在”的性质,赋予了一个已经存在的、可能是任意选择的个体,这是非法的逻辑跳跃。
证法2:教科书级别的精准破案
证法2的破案流程:
(∃x)P(x)– (华生的情报先进来了:“有一个凶手!”)P(a)– (ES/EI) 福尔摩斯说:“很好。我们不知道他是谁,但为了讨论方便,我们给他起个代号,就叫他‘嫌疑人a’。”
- 这一步非常关键。
a在这里第一次出现,是作为一个全新的、专门指代那个“存在的凶手”的代号。我们现在有了一个坚实的基础:a就是那个凶手。(∀x)(P(x) →Q(x))– (现在拿出我们的铁律)P(a) →Q(a)– (US/UI) 福尔摩斯把铁律应用到我们锁定的“嫌疑人a”身上:“既然这条铁律对‘任何凶手’都成立,那它必然也对我们眼前这位‘嫌疑人a’成立。所以,如果a是凶手,他口袋里就有火车票。”
- 这一步合法。UI可以应用到任何个体,当然也包括我们刚刚用EI引入的
a。Q(a)– (T, 也就是肯定前件Modus Ponens) 好了,我们有两条信息:
- (2)
a就是凶手 (P(a))- (4) 如果
a是凶手,他就有票 (P(a)→Q(a))- 结论显而易见:
a口袋里有火车票!(Q(a))(∃x)Q(x)– (EG) 既然我们已经找到了一个确定的人(a),他口袋里有火车票,那我们当然可以得出结论:“存在某个人,他口袋里有火车票。” 结案!
总结:黄金法则
为了避免制造冤假错案,请务必遵守这条谓词演绎的黄金法则:
能先用 EI,就一定要先用 EI! (EI First!)
道理很简单: EI规则的限制最严格(必须引入新符号),你得先处理掉这个最麻烦、最受限的步骤。一旦你把那个“存在的家伙”用一个新代号(比如
a)固定下来了,你手里就多了一个可以使用的“具体的人”。然后,你就可以随心所欲地把那些限制宽松的UI规则(“对所有人都成立”)应用到这个新出现的人身上了。
公式的等价
问:量词分配律为什么必须要满足
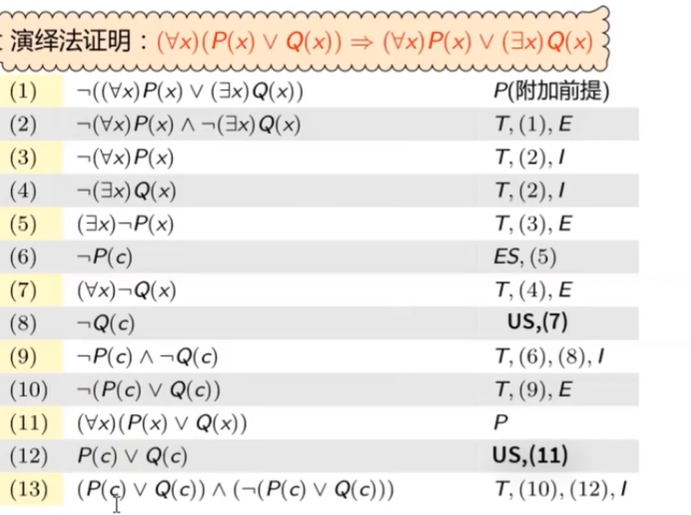
\((\forall x)(G(x) \land H(x)) = (\forall x) G(x) \land (\forall x) H(x);\)
\((\exists x) (G(x) \lor H(x)) = (\exists x) G(x) \lor (\exists x) H(x)\)
把合取换成并取 或 更变量词后,就是错误的,请解释,可以的话,结合理论逻辑和事实实例,证明该定理
回答1:
咱们先把这两个量词想象成两个人:
- 全称量词 ∀ (For All):这家伙是个“完美主义者”,看问题特别严格,要求每个人都必须满足条件,一个都不能少。
- 存在量词 ∃ (Exists):这家伙是个“乐天派”,看问题很宽松,只要至少有一个人满足条件,他就心满意足了。
好,现在我们来破案,看看为什么有的组合是天作之合,有的却是八字不合。
Part 1: 天作之合的组合 (为什么它们是对的)
1. ` (∀x)(G(x) ∧ H(x)) <=> (∀x)G(x) ∧ (∀x)H(x) `
- 左边
(∀x)(G(x) ∧ H(x))的意思是:
- 对于每一个人x,他都同时满足G和H两个条件。
- 实例:假设一个班级(论域)里的学生x。G(x)是“x通过了数学考试”,H(x)是“x通过了语文考试”。
- 左边的意思就是:“班上每一个人,都既通过了数学,又通过了语文。”
- 右边
(∀x)G(x) ∧ (∀x)H(x)的意思是:
- (班上所有人都通过了数学)并且(班上所有人都通过了语文)。
- 这是分两步检查,但要求同样严格。先查数学成绩,是不是所有人都过了?再查语文成绩,是不是所有人都过了?两个都是,才算对。
- 为什么相等?
- 你想想,如果班上每个人都是“数学语文双优生”,那必然“全班数学都及格”和“全班语文都及格”这两个结论都成立。反过来也一样。逻辑上是完全等价的。所以,“完美主义者”和“并且”是好朋友,它们的要求可以叠加。
2. ` (∃x)(G(x) ∨ H(x)) <=> (∃x)G(x) ∨ (∃x)H(x) `
- 左边
(∃x)(G(x) ∨ H(x))的意思是:
- 存在某个人x,他满足G或者满足H(或者都满足)。
- 实例:还说这个班。G(x)是“x是体育特长生”,H(x)是“x是艺术特长生”。
- 左边的意思就是:“班里至少有一个人,他要么是体育特长生,要么是艺术特长生。” 只要我能找到一个就行,不管是哪种。
- 右边
(∃x)G(x) ∨ (∃x)H(x)的意思是:
- (班里至少有一个体育特长生)或者(班里至少有一个艺术特长生)。
- 这也是分两步找。我先去体育生里找,找到了吗?或者我去艺术生里找,找到了吗?只要任何一边找到了人,就算任务完成。
- 为什么相等?
- 如果我找到了一个“身兼两职”的人,那左右两边肯定都成立。如果我找到了一个纯粹的体育生,那左边成立(因为满足“或”),右边也成立(因为“至少有一个体育生”)。逻辑上也是完全等价的。所以,“乐天派”和“或者”是好搭档,它们的目标都是“大海捞针”,只要捞到一根就行。
Part 2: 八字不合的组合 (为什么它们是错的)
现在到了最关键的地方,为什么把联结词换一下,这事儿就“拧巴”了呢?
3. ` (∀x)(G(x) ∨ H(x)) ` 不等于 ` (∀x)G(x) ∨ (∀x)H(x) `
- 左边
(∀x)(G(x) ∨ H(x))的意思是:
- 每一个人,都要么满足G,要么满足H。
- 实例:论域是“一群人”。G(x)是“x是男性”,H(x)是“x是女性”。
- 左边的意思就是:“这里每一个人,要么是男的,要么是女的。” 这句话显然是真的(不考虑特殊情况)。它允许张三是男的,李四是女的。它只对个体有要求,没对全体有统一要求。
- 右边
(∀x)G(x) ∨ (∀x)H(x)的意思是:
- (所有的人都是男性)或者(所有的人都是女性)。
- 这句话的意思是,这个群体要么是“全男性”团体,要么是“全女性”团体。在一个男女混合的群体里,这句话显然是假的。
- 为什么不等?
- 你看,左边说的是“每个人都有个身份就行”,而右边说的是“所有人都得是同一个身份”。要求强度完全不同! 左边真的时候,右边可能是假的。所以它们不相等。
- 逻辑上,箭头只能单向成立:
(∀x)G(x) ∨ (∀x)H(x) → (∀x)(G(x) ∨ H(x))。如果一个地方全是男的,那确实满足“每个人要么是男要么是女”。但反过来就不成立了。
4. ` (∃x)(G(x) ∧ H(x)) ` 不等于 ` (∃x)G(x) ∧ (∃x)H(x) `
- 左边
(∃x)(G(x) ∧ H(x))的意思是:
- 存在一个人,他同时满足G和H。
- 实例:论域是“一个篮球队”。G(x)是“x会投三分”,H(x)是“x会扣篮”。
- 左边的意思就是:“队里至少有一个人,既会投三分,又会扣篮”。我们要找的是一个“全能选手”。
- 右边
(∃x)G(x) ∧ (∃x)H(x)的意思是:
- (队里至少有一个人会投三分)并且(队里至少有一个人会扣篮)。
- 这句话的意思是,队里有个“三分射手”(比如库里),同时还有个“扣篮王”(比如奥尼尔),但这俩人可以不是同一个人。
- 为什么不等?
- 很明显,左边要求找到一个“超人”,而右边只要找到一个“射手”和一个“壮汉”就行了。右边的条件比左边宽松太多了!
- 可能我们队里,A只会投三分,B只会扣篮。这时,右边是真的(因为我们找到了A和B),但左边是假的(因为我们找不到任何一个全能的人)。
- 逻辑上,箭头也只能单向成立:
(∃x)(G(x) ∧ H(x)) → (∃x)G(x) ∧ (∃x)H(x))。如果队里有个全能王,那当然满足“队里有会三分的”并且“有会扣篮的”。但反过来就不成立了。
总结一下,帮你记牢
- ∀ (完美主义者):它的权力很大,能把自己的严格要求“分配”给
∧(并且) 的每一项,因为∧也是个严格的家伙。但它不能分配给∨(或者),因为∨会让它的严格要求“打了折扣”。- ∃ (乐天派):它的要求很低,能把自己的宽松要求“分配”给
∨(或者) 的每一项,因为∨也是个宽松的家伙。但它不能分配给∧(并且),因为∧会突然拔高它的要求,让它“不堪重负”。
蕴含推理
问:蕴含符号的问题,$\implies$和$\rightarrow$ 有什么区别?
答:
$\implies$表示公式之间的关系,如等价、蕴含
$\rightarrow$是运算符号,代表蕴含的逻辑运算符
问:为什么 (∀x)G(x) ∨ (∀x)H(x) => (∀x)(G(x) ∨ H(x))?
答:
(∀x)G(x) ∨ (∀x)H(x) => (∀x)(G(x) ∨ H(x))
这个公式说的是:如果左边成立,那么右边一定成立。
咱还是用“班级及格”那个例子来走一遍,你就明白了为啥这次行得通。
前提: 咱们假设左边
(∀x)G(x) ∨ (∀x)H(x)是真的。
一个 “或” (∨) 命题是真的,意味着什么?意味着它连接的两件事,至少有一件是真的。所以,我们现在有两种可能的情况(或者两种都发生):
- 情况一:
(∀x)G(x)是真的。
- 翻译过来就是:“全班体育都及格了”。
- 在这种情况下,我们再看右边
(∀x)(G(x) ∨ H(x))是不是真的。右边的意思是:“班里的每一个人,都至少及格了一门课”。- 既然全班体育都及格了,那班里随便拉出来一个人,他肯定体育及格了,那他自然也就满足“至少及格一门”这个条件。所以,在这种情况下,右边是真的。
- 情况二:
(∀x)H(x)是真的。
- 翻译过来就是:“全班美术都及格了”。
- 同理,既然全班美术都及格了,那班里随便拉出来一个人,他美术肯定及格了,所以他也满足“至少及格一门”这个条件。因此,在这种情况下,右边也是真的。
结论:
你看,只要左边的前提
(∀x)G(x) ∨ (∀x)H(x)成立,不管是哪种情况(全班过体育,或者全班过美术),都能百分之百地推导出右边(∀x)(G(x) ∨ H(x))也成立。
所以,这个从左到右的单向箭头是没问题的。
小Z给你个直观的总结
这其实是一个“强条件能推出弱条件”的经典案例。
- 左边
(∀x)G(x) ∨ (∀x)H(x)是一个非常强的条件。 它要求整个班级要么在体育上“整齐划一”,要么在美术上“整齐划一”。这是个很高的要求,很难达成。- 右边
(∀x)(G(x) ∨ H(x))是一个相对弱的条件。 它只要求每个人自己“管好自己”,保证自己别两门都挂科就行。它允许班级内部存在“偏科”的学生。
一个如此强大的、要求“全体一致”的条件如果都达成了,那后面那个只要求“人人过关”的弱条件,自然也就在情理之中地达成了。
但反过来就不行,就像我们上次聊的,右边的弱条件(人人都至少过一门)是推不出左边的强条件(全班都过了某一门)的。